
风险比(hazard ratio,HR)和中位生存时间是生存分析时的常规分析和报告指标。本文简要介绍了HR和中位生存时间的关系以及比例风险假定在这两者之间的作用,分析了检索出的58篇文献中的110对风险比和中位生存时间比的差异,并通过实例阐明了产生这种差异的原因。结果表明,在不满足比例风险假定时,Cox回归模型计算得到的风险比是不合理的,且与中位生存时间之比不等价。因此,在使用Cox回归模型前,应先进行比例风险假定的检验,只有符合比例风险假定时才能使用该模型;当不符合比例风险假定时,建议使用限制性平均生存时间。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
在生存分析中,风险比(hazard ratio,HR)和中位生存时间是两种最常用的效应指标。由于风险比可以从Cox回归模型中轻松获得,一直以来是研究者们常用的衡量指标。然而Cox回归模型的应用需满足比例风险的假设,但研究者们却忽略了这一点,导致风险比被滥用。中位生存时间是基于时间的度量指标,很容易从Kaplan-Meier曲线中估算出来,我们可以使用中位生存时间之比(median ratio,MR)来比较两组研究对象的生存获益程度。从理论上讲,如果两组研究对象事件发生率随时间变化是恒定的,风险比和MR将是等价的,否则风险比与MR并不等价。鉴于风险比与中位生存时间在生存分析中的重要性,本文将介绍风险比和中位生存时间的关系以及比例风险假设在两者关系中的作用,并利用实例检索展示和诠释风险比和中位生存时间的关系,同时提出在不满足比例风险假定的情况下衡量生存收益的方法。
风险比是一组研究对象发生某特定事件的瞬时风险与另一组研究对象发生某特定事件的瞬时风险之比。中位生存时间是刚好有50%的个体发生某特定事件的时间。从理论上来说,只有当两组对象发生某特定事件的概率随着时间的变化是恒定的,即风险比是恒定的,才能估计出一个固定的风险比,这种情况下风险比和中位生存时间之比是等价的,风险比和中位生存时间可以互相推导。以评估干预措施延长生存期的随机对照临床试验为例,干预组与对照组的死亡风险比是0.5,即从开始治疗至随访结束的任何一个时刻干预组的死亡风险是对照组的0.5倍,那么50%干预组患者发生死亡的时间是50%对照组患者发生死亡时间的2倍,即干预组的中位生存时间是对照组的2倍。风险比是一个相对效应指标,仅仅反映治疗组和对照组相比死亡发生的可能性大小;若要反应干预措施能在多大程度上延长生存时间,则需要绝对效应指标中位生存时间。假设风险比和中位生存时间之比等价,治疗组和对照组的死亡风险比是0.25,这是一个非常可观的效应指标,但是绝对效应不一定理想。死亡风险比是0.25意味着治疗组的中位生存时间是对照组的4倍,而治疗的绝对收益取决于对照组的生存期,若对照组的中位生存时间是7 d,治疗组的中位生存时间也就28 d,21 d的疗效差别并不可观;如果对照组的中位生存时间是7年,则治疗组可以延长21年的生存期则相当可观。
风险比通常是利用Cox比例风险模型估计出的一个固定值,显然要求风险比从研究开始至随访结束的任何一个时刻都是恒定的,也就是说两组研究对象的生存曲线是平行无交叉的,这就是Cox比例风险模型的比例风险假定(proportional hazard assumption,PH),简称PH假定。在使用Cox比例风险模型估计风险比之前,需要进行比例风险假定的检验,只有在满足比例风险假定的情况下,使用Cox比例风险模型才是合理的。在现实中,即使符合比例风险假定,也不意味着任何时刻的风险比都是完全一致的,只能说明它们是近似的,所以风险比和中位生存时间之比多数情况下是近似的,只有在最理想的情况下才是完全相同的。在不符合比例风险假定的条件下估计出风险比是不合理的,尤其是当生存曲线存在交叉的时候,在交叉点之前和之后的风险比是相反的,这种情况下估计出的HR值是一个平均值,不能反映客观真实的情况,不能和中位生存时间之比等价。例如,接受免疫治疗的小部分患者会表现出特殊的应答模式:延迟反应和假性进展,这可能会导致在治疗前期接受免疫治疗患者死亡或者疾病进展的风险高于对照组,而在某个交叉点之后免疫治疗患者死亡或者疾病进展的风险低于对照组的情况。这种情况下可能需要以交叉点为界,分别估计两组研究对象某事件的风险比。研究表明,当生存曲线存在交叉的时候,估计出的总体风险比和中位生存时间之比差异很大,20%(25/128)的试验中的风险比和中位生存时间之比是相反的,即风险比表明治疗是有益的,中位生存时间之比表明是有害的,反则亦然[1]。在很多情况下,我们不知道研究中的数据是否符合比例风险假定,这种情况下我们要同时关注风险比和中位生存时间,根据具体情况作出判断。
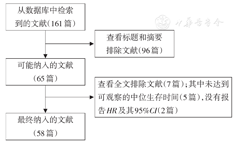
利用PubMed检索平台检索2014年1月至2018年12月发表在新英格兰医学杂志的肿瘤治疗领域的随机对照临床试验,关键词为:Neoplasms、Cancer、Carcinoma、Tumor、Cox和Hazard等,检索截至时间为2018年12月29日。检索限制在人类研究。纳入的研究是随机对照试验的全文报告。文献的纳入标准为:(1)癌症研究;(2)研究中有生存曲线的数据;(3)随机对照临床试验。排除标准为:(1)未观察到中位生存时间;(2)没有报告总生存期(overall survival,OS)和无进展生存期(progression-free survival,PFS);(3)没有报告HR及其95%CI值的文献。根据纳入和排除标准对检索到的文献进行筛选。从合格的文献中摘录题目、发表年份、中位总生存期和/或中位无进展生存期、HR及其95%CI值和样本量。共检索到161篇文献,根据摘要和标题筛查中排除96篇文献,全文筛查中排除无HR及其95%CI值的文献2篇,排除未观察到中位生存时间的文献5篇。最终共纳入58篇文献。文献检索和筛选流程图见图1。

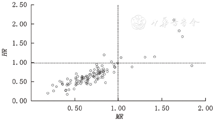
在检索到的58篇文献中,共收集到110个HR-MR对子,经配对样本t检验结果表明:在α=0.05的水平上,两组差异有统计学意义(t=2.311,P=0.023)。其中HR与MR数值大小完全相等的对子数有7个(6.36%,7/110),HR与MR方向相反(即MR>1而HR<1或MR<1而HR>1)的对子数有4个(3.63%,4/110),中位生存时间与风险比之间的散点图如图2所示,相关系数为0.86(P<0.01)。

以Finn等[2]的研究为例,该试验比较了来曲唑联合帕布昔利布与单独使用来曲唑对晚期乳腺癌患者的疗效,样本量为666人,中位随访时间为23个月。图3显示了研究人员评估的晚期乳腺癌患者接受治疗后的中位无进展生存时间曲线图,是HR与MR完全一致的实例。从图中可以看出,来曲唑联合帕布昔利布组的中位无进展生存时间为24.8个月,而来曲唑组的中位无进展生存时间为14.5个月,MR为0.58(14.5/24.8),而HR为0.58(95%CI为0.46~0.72)。观察两条生存曲线发现,两条曲线趋势基本一致,且无交叉,符合风险比例假定[3]。因此在不违反比例风险假定的前提下,HR与MR表现出良好的一致性。
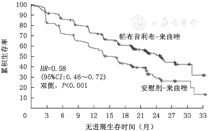

表1描述了4篇[4,5,6,7]HR与MR不一致论文的基本信息,包括第一作者、发表年份、样本量大小、HR(95%CI)、两组中位生存时间、MR等。这四篇论文的HR和MR的点估计值都分别指向了不同的方向。
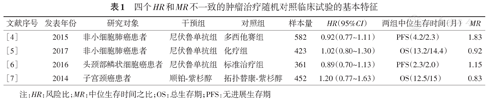
四个HR和MR不一致的肿瘤治疗随机对照临床试验的基本特征
四个HR和MR不一致的肿瘤治疗随机对照临床试验的基本特征
| 文献序号 | 发表年份 | 研究对象 | 干预组 | 对照组 | 样本量 | HR(95%CI) | 两组中位生存时间(月) | MR |
|---|---|---|---|---|---|---|---|---|
| [4] | 2015 | 非小细胞肺癌患者 | 尼伏鲁单抗组 | 多西他赛组 | 582 | 0.92(0.77~1.11) | PFS(4.2/2.3) | 1.83 |
| [5] | 2017 | 非小细胞肺癌患者 | 尼伏鲁单抗组 | 化疗组 | 423 | 1.02(0.80~1.30) | OS(13.2/14.4) | 0.92 |
| [6] | 2016 | 头颈部鳞状细胞癌患者 | 尼伏鲁单抗组 | 标准治疗组 | 361 | 0.89(0.70~1.13) | PFS(2.3/2.0) | 1.15 |
| [7] | 2014 | 子宫颈癌患者 | 顺铂紫杉醇 | 拓扑替康紫杉醇 | 452 | 1.20(0.77~1.63) | OS(12.5/15) | 0.83 |
注:HR:风险比;MR:中位生存时间之比;OS:总生存期;PFS:无进展生存期
图4是上述4篇论文中两组研究对象不同结局的生存曲线图。图4A是比较尼伏鲁单抗组和多西他赛治疗非小细胞肺癌患者PFS疗效的生存曲线图,图4B是比较尼伏鲁单抗与化疗对非小细胞肺癌患者OS疗效的生存曲线图,图4C是比较尼伏鲁单抗与标准化治疗对头颈部鳞状细胞癌患者PFS疗效的生存曲线图,图4D是比较无论是否使用贝伐单抗的顺铂-紫杉醇(CP)化疗患者和无论是否使用贝伐单抗的拓扑替康-紫杉醇(TP)化疗对子宫颈癌患者OS疗效的生存曲线图。从它们的生存曲线图可以看出,这4项研究的共同特征是生存曲线在某一点上相互交叉,明显违反了比例风险假定。这四项研究均是肿瘤免疫治疗实验,正如在免疫治疗试验中经常看到的,生存曲线呈现出延迟反应模式。两组之间生存曲线的早期重叠表明治疗在早期没有表现出其全部效果,但对患者也没有伤害,超过一定的时间点后,两条曲线开始分开,表现出免疫治疗组优于对照组的情况。这意味着免疫治疗的效果在用药后的不同时间段不同,导致免疫治疗的两组生存曲线往往不满足比例风险假设,因而HR和MR得出了两种完全不同的结论。
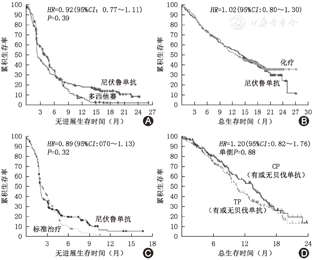

由上述理论和实例分析可知,在不满足风险比例假定时,尤其是当生存曲线存在交叉时,HR与MR之间的数值一般是不一致的,HR与MR不能相互推导。在违反了PH假定的情况下,特别是生存曲线交叉时,此时HR随着时间的变化而变化,我们不能简单应用Cox比例风险模型估计HR值,否则可能得出与实际问题不符的解释,甚至是HR与MR方向相反的结果(即MR>1而HR<1或MR<1而HR>1)。Cox比例风险模型已经被广泛应用于生存分析中,这个模型仅在比例风险假定成立的条件下才有效,然而这个假定却很少被检验,误用和滥用Cox比例风险模型的现象屡见不鲜。新英格兰杂志中的一篇文献中指出[8],大部分免疫治疗研究都没有进行PH假定,从而导致了对HR的错误解读。
国外已有一部分文献提醒研究人员注意非PH的可能性,并提出了如何分析这些数据的方法。许多研究建议在不满足比例风险假定的情况下,可以采用限制性平均生存时间(restricted mean survival times,RMST)代替HR[9,10,11]。RMST指的是生存曲线在某个时间段的曲线下面积,即平均的生存时间。RMST及其标准差可以通过SAS的PROC LIFETEST过程计算得到,见表2。Trinquart等[12]认为相比于传统的Cox模型,RMST不依赖于比例风险假定,结果直观且容易理解。Dehbi等[13]3位医学统计学家建议,当风险比随时间变化时,可以使用试验组与对照组的RMST之差,即预期寿命差(life expectancy difference,LED),和试验组与对照组的RMST之比,即预期寿命比(life expectancy ratio,LER)作为衡量治疗效果的绝对指标和相对指标;该指标可以解释为由于干预导致的预期寿命的绝对或相对延长(或损失)。当生存曲线存在交叉时,他们建议在曲线交叉点之前或之后,分别报告两个LED和LER估计值,以区分早期和晚期治疗效果。因此,RMST作为一种有意义且敏感的结果分析方法,具有巨大潜力。当我们无法确信比例风险假定是否成立时,RMST可能是很好的衡量指标。
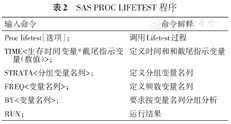
SAS PROC LIFETEST程序
SAS PROC LIFETEST程序
| 输入命令 | 命令解释 |
|---|---|
| Proc lifetest[选项]; | 调用Lifetest过程 |
| TIME<生存时间变量*截尾指示变量(数值)>; | 定义时间和和截尾指示变量 |
| STRATA; | 定义分组变量名列 |
| FREQ; | 定义频数变量名列 |
| BY; | 要求按变量名列分组分析 |
| RUN; | 运行结果 |
综上所述,HR与MR并不总是一致的。在忽略比例风险假定的前提下,Cox比例回归模型得出的HR值会掩盖治疗效果的真实特性,此时得出的HR与MR会不一致。因此,在进行Cox比例回归模型前应先进行比例风险条件检验,若检验成立则计算得出的HR值可信度高,否则得出来的衡量指标可能会误导临床决策。
所有作者均声明不存在利益冲突
1.风险比指的是:
A.两种不同条件下死亡概率之比
B.两种不同条件下生存概率之比
C.两种不同条件下的危险率函数之比
D.死亡率与生存率之比
E.死亡概率与生存概率之比
2.Cox比例回归模型要求两个不同个体在不同时刻t的风险函数之比:
A.随时间增加而增加
B.随时间增加而减小
C.开始随时间增加而增加,后来随时间增加而减小
D.不随时间改变
E.视具体情况而定
3.以下关于生存分析中几个基本概念的描述错误的是:
A.中位生存时间是恰有50%的观察对象发生特定事件的时间
B.生存率是指某一观察对象能生存过或活过t时点的概率
C.生存时间是指从随访观察起点到随访截止时点的时间
D.在生存分析中,随访终止时间一定是全部观察对象发生研究事件(如死亡)的时间
E.生存分析是同时考虑事件观察结果及随访时间的一种统计分析方法
4.在进行Cox回归模型前,应先进行以下哪个检验?
A.比例风险假定检验
B.t检验
C.Z检验
D.χ2检验
E.无须进行任何检验
5.在不满足比例风险假定的情况下,可采用以下哪种指标?
A.风险比
B.中位生存时间
C.限制性平均生存时间
D.生存率
E.以上皆可



























