
logistic回归是研究一个二分类或多分类反应变量与多个影响因素之间关系的多因素分析方法,它由一族回归模型组成,包括二分类结果的多重logistic回归、配对资料的条件logistic回归、多分类结果的logistic回归、有序结果的累积优势logistic回归和有序结果的相邻优势logistic回归。本文从实际应用的角度出发,介绍多重logistic回归分析方法,包括模型原理、自变量筛选及赋值、应用条件、模型评价和模型诊断等内容,也阐述了多分类结果变量的logistic回归和有序结果的累积优势logistic回归的原理和应用,并结合实例给出SAS程序和结果解释,以帮助读者掌握logistic回归分析方法,在科研和工作实践中能正确使用,以提高数据使用效率和统计分析水平。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
医学研究经常会遇到结局变量是分类变量,比如是否患有糖尿病等慢性病;手足口病的密切接触者是否发病;家长是否使用安全座椅;某种治疗手段后的疾病结局是无效、控制、好转或治愈等。当分析上述问题与多个危险因素之间的关系时,应该采用logistic族回归模型。logistic回归是研究一个二分类或多分类反应变量与多个影响因素之间关系的多重回归分析方法,它由一族回归模型构成,包括多重logistic回归、条件logistic回归、多分类结果的logistic回归、有序结果的累积优势logistic回归和有序结果的相邻优势logistic回归[1]。logistic回归主要用于探索疾病发生的危险因素,在众多因素中筛选出主要的危险或保护因素;控制混杂因素和分析交互作用;确定自变量对因变量影响相对重要性;利用回归模型计算结局发生的概率,对结局做出概率性的预测[2,3]。
logistic回归模型的反应变量y是分类变量,本文以结局变量为二分类的多重logistic回归为例,介绍模型的基本原理。
当反应变量y是二分类变量时,以研究者所关注的结局发生概率为π,如患病、死亡、就医等,与之对立或相反的结局发生概率则为1-π,多重logistic回归方程可写成:
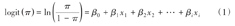
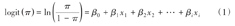
其中:i为自变量的个数;β0为截距或常数项,表示各自变量取值为0时,logit (π)的总体均数;β1, β2, …, βi为偏回归系数(简称回归系数),表示当其他自变量保持不变时,xi增加或减少一个单位时,logit (π)的平均变化量。
从式1可知,logistic回归方程右侧x1~xi的线性组合与多重线性回归是一样的[4],取值区间为(-∞, +∞);而方程左边是结局事件发生概率的 。
。 称为logit变换,π的取值区间为[0, 1]的概率。π通过logit转换后,logit (P)取值区间为(-∞, +∞),与方程右边线性组合的取值区间一致。
称为logit变换,π的取值区间为[0, 1]的概率。π通过logit转换后,logit (P)取值区间为(-∞, +∞),与方程右边线性组合的取值区间一致。
式1经过转换,可以得到logistic回归模型另外一种表达形式:
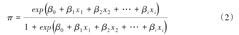
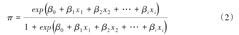
可用来估计当β1, β2, …, βi取某一组确定数值时,结局事件发生概率π。
logistic回归模型中的回归参数,通常采用极大似然估计(maximum likelihood estimation, MLE),利用样本数据求解得到发生样本结局的可能性最大的b1, b2, …, bi值,作为β1, β2, …, βi的估计值。logistic回归模型需要进行假设检验,分别检验回归模型是否成立和模型参数是否有统计学意义。回归模型检验的无效假设为β1=β2=…=βi=0,即所有解释变量的偏回归系数均为0,检验方法包括似然比检验、计分检验和Wald检验;模型参数检验的无效假设为βi=0,即某一解释变量的偏回归系数为0,可用Wald卡方检验。以上检验统计软件均给出计算结果。
如前所述,回归系数βi表示当其他自变量保持不变时,xi增加或减少一个单位时logit (π)的平均变化量。实际上,logit (π)的专业意义并不直接,但通过数学转换,可以将回归系数βi转化为流行病学研究中的比值比(odds ratio, OR),两者之间的数学关系为OR=exp(βi)。OR值反映了暴露与结局的关联强度,从这个角度可以给予回归系数βi更清晰的专业意义:当βi=0时,OR=1,表示因素xi暴露和结局之间不存在关联;当βi>0时,OR>1,提示xi为危险因素,会增加结局事件发生的危险;当βi<0时,OR<1,提示xi为保护因素,会降低结局事件发生的危险。
在logistic回归分析中,自变量的赋值是一个关键的环节[5]。不同的变量赋值形式可能导致回归模型参数的符号、大小和含义发生变化。分析中自变量包括分类变量、等级变量和连续变量三类,变量赋值形式各有不同。
性别、是否有家族史、是否吸烟等为二分类变量,在数据整理时通常用0和1表示,可以直接纳入logistic回归分析,得到暴露(1)与非暴露(0)相比的OR值。
职业、学历、血型等多分类变量,在数据整理时通常用1,2,3,…,k表示k个不同的类别。这里的数值只是分类的一个代码,无大小关系,需要将取值范围为k的分类变量转化成k-1个哑变量(dummy variable)纳入回归模型。每个哑变量都是一个二分类变量,用0和1表示,得到1与0相比的OR值。表1是以血型(type)中的O型为参照组进行哑变量变换,生成type1、type2、type3三个哑变量,分别代表A、B或AB三种血型。注意:在拟合模型时哑变量同时纳入模型或同时移出模型,如血型有三个哑变量type1、type2和type3,应同时纳入回归模型。
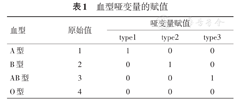
血型哑变量的赋值
血型哑变量的赋值
| 血型 | 原始值 | 哑变量赋值 | ||
|---|---|---|---|---|
| type1 | type2 | type3 | ||
| A型 | 1 | 0 | 0 | |
| B型 | 2 | 1 | 0 | |
| AB型 | 3 | 0 | 1 | |
| O型 | 4 | 0 | 0 | |
人体血清反应强度(-, +, ++, +++)、药物治疗的效果(治愈、显效、好转、无效)等变量具有等级性,在数据整理时也通常整理为1,2,3,…,k的数值型变量,其数值大小代表了等级关系。在进行logistic回归分析时,等级变量可以以连续变量的形式进入回归模型,得到自变量每改变1个等级时的OR值。但这样处理的前提条件是自变量的等级分组与阳性结果的改变情况呈线性关系,其效应呈等比例改变(检验见下文)。如果该前提不满足,则只能将等级变量作为分类变量,用哑变量进行分析。
年龄、血压、白细胞计数等在数据整理时一般以原始观察值记录。如将连续变量直接带入logistic回归,则OR值表示自变量每改变1个单位,阳性结果的发生情况是前一个水平的倍数。这种情况有时在专业上比较难理解,比如年龄,OR值表示每增加1岁时的改变情况,不一定具有临床意义。此时应将变量按值大小分成几组,按等级变量纳入分析,在不满足线性假设的情况下,则应按照分类变量做哑变量处理,纳入模型分析。
例1:为了解肥胖的影响因素,研究者随机抽取了某社区40岁及以上居民500人进行问卷调查,收集了调查对象的性别(sex)、文化程度(edu)、吸烟(smo)和家族史(his)等因素,并测量了调查对象的身高(height,单位为m)、体重(weight,单位为kg)和血压[bp,单位为mmHg(1 mmHg=0.133 kPa)],通过计算体重指数(body mess index, BMI)判断调查对象的肥胖情况。变量赋值情况见表2。其中性别、吸烟、家族史为二分类变量,文化程度为多分类变量,血压为连续型变量。

肥胖影响因素研究变量赋值表
肥胖影响因素研究变量赋值表
| 变量名称 | 分类及编码 |
|---|---|
| 性别(sex) | 0=女性,1=男性 |
| 文化程度(edu) | 1=小学及以下,2=初中,3=高中/中专/技校,4=大专及以上 |
| 吸烟(smo) | 0=否,1=是 |
| 家族史(his) | 0=无,1=有 |
| 血压(bp) | 连续变量 |
| 肥胖(obe) | 0=否,1=是 |
本研究结局变量肥胖(obe)为二分类变量,研究目的是探索多个自变量对因变量影响,应采用logistic回归进行分析。性别(sex)、吸烟(smo)、家族史(his)为二分类变量,直接纳入分析;文化程度为多分类变量,以哑变量纳入分析,参考组为1(小学及以下);血压为连续型变量,应按值大小分组,本研究以大于等于140 mmHg为高血压判定标准,将血压转化为二分类变量(0=非高血压,1=高血压)纳入分析。
变量转化的SAS程序:
data mnsj1;
set mnsj;
if bP<=140 then bp_1=0;else bp_1=1;
run;
logistic回归分析的SAS程序:
PROC LOGISTIC data=mnsj1 desc;
CLASS edu (param=reference ref=first);
MODEL obe=sex edu smo his bp_1;
RUN;
其中:PROC logistic调用logistic回归分析模块;desc将SAS程序默认结果变量的较小值与较大值的比较改为较大值与较小值的比较;Class通过param=reference和ref=first产生以第一类为参照组的虚拟变量,参考组还可定义last或"某类别赋值";MODEL定义回归模型,obe为因变量,sex、edu、smo、his、bp_1为自变量。通过selection=指定变量选择方法,包括前进法(forward)、后退法(backward)、逐步法(stepwise)、最优子集法(scores)等,默认为none,即列出的自变量全部纳入模型。本研究强制纳入研究者感兴趣的全部自变量,不指定变量选择方法。
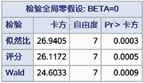

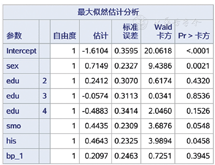

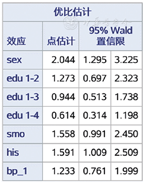

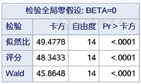
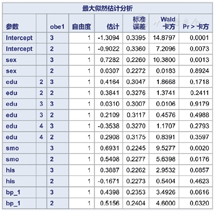
图1是回归模型检验结果,P<0.05表示回归模型成立;图2是模型参数检验结果,按照0.05的水准,性别(sex)、吸烟(smo)、家族史(his)有统计学意义,文化程度(edu2、edu3、edu4)、高血压(bp_1)无统计学意义。在分析中要结合专业知识和研究假设决定是否去掉文化程度和高血压重新建立模型,本文不再赘述,自变量筛选策略见参考文献[3]。
以上述拟合结果为例建立logistic回归方程:
logit(P)=-1.610 4+0.714 9sex+0.241 2edu2- 0.057 4edu3- 0.488 3edu4+0.443 5smo+0.464 3his+0.209 7bp_1。
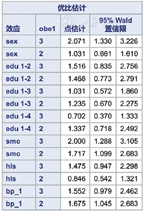
图3是效应值估计结果,从中可知:男性是肥胖的危险因素,相对于女性的OR值为2.044;吸烟是肥胖的危险因素,相对于不吸烟的OR值为1.558;家族史是肥胖的危险因素,相对于无家族史的OR值为1.591;尚不能认为文化程度和高血压与肥胖有关联。
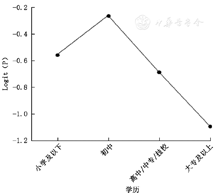
进行logistic回归分析之前,首先需要对模型的应用条件独立性和线性进行检验。独立性是指因变量取值之间相互独立,一般用专业知识进行判断。线性是指logit (P)与自变量符合线性关系。当自变量为二分类变量时,不需要进行线性验证;当自变量为等级变量或连续型变量时,可通过绘制自变量与logit (P)的关系图进行判断。以例1的文化程度(edu,等级变量)为例,SAS程序及结果如下:
ODS graphics on;
PROC LOGISTIC data=mnsj1 desc plots(only)=(effect(link join=yes));
CLASS edu;
model obe=edu;
RUN;
从图4可见,等级变量edu的增加与logit(P)无线性关系,此时edu不能以线性分组变量纳入模型,需要以哑变量的形式纳入模型。具体方法见前面的叙述。

模型估计完成后要评价模型的优劣,在拟合的多个模型中选择拟合效果相对更优的模型。Pearson χ2、Deviance、HL(Hosmer-Lemeshow)统计量用于评价模型与样本数据的匹配程度,值越小,表示模型的预测值与对应的观测值的一致性越好,拟合效果越好。广义决定系数R2和校正决定系数Radj2表示自变量对因变量的解释能力,值越大,自变量对因变量的解释能力越强。AIC和SC值用于同一数据的多个模型之间的拟合优度比较,值越小表示模型拟合越好。见图5。SAS程序如下:
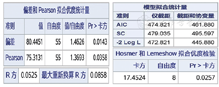

PROC LOGISTIC data=mnsj1 desc;
CLASS edu(param=reference ref=first);
MODEL obe=sex edu smo his bp_1/aggregate scale=none lackfit rsquare;
RUN;
回归模型的应用条件或因变量和自变量的数据结构存在问题,可能导致有偏或者精度差的估计。模型诊断主要包括异常点(如离群点、高杠杆点、强影响点)、多重共线性、空单元格、完全分离、过度离散等[6]。异常点和多重共线性的诊断与多重线性回归相同[4],本文不再赘述。
空单元格是自变量各水平的交叉列联表中有些单元(格子)的观测频数为0,此时易产生一个0或者∞的OR值,变量的效应无法合理解释。当出现以上情况时,可通过自变量组合的列联表查看是否存在空单元格,并通过增加样本含量、与其相邻类合并、去除该类,或改用精确logistic回归模型(exact logistic regression model)进行处理。
完全分离是自变量xi存在一个临界值c,当xi≥c时事件发生,xi<c时则事件不发生,结局变量的两种结果在取值上无任何重叠。完全分离与样本含量的大小、事件发生的例数、模型中自变量的数目及自变量的取值范围有关。若出现估计系数很大,尤其是系数估计标准误非常大的时候,应分析是否有完全分离的情况发生,并根据发生原因解决问题。
过离散(over-dispersion)是指测量方差大于期望方差,主要出现于聚集现象或非独立数据。过离散会导致参数估计的标准误低,造成假阳性错误。在没有过离散的情况下,模型评价的Pearson χ2和Deviance指标值与自由度的比值均等于1或接近1,如果这两个比值距离1较远,提示可能存在过离散现象。在前述的logistic拟合程序中,可将scale=none改为scale=Pearson或scale=Deviance进行调整。
多分类结果的logistic回归(polytomous logistic regression)利用的多项logit模型,主要用于处理结局变量为无序多分类的情形[1,7]。由于结局变量有多个分类,因此构成的模型不止一个,而是与结局变量的分类数量相关。如果结局变量有k个分类,就会产生k-1个模型。多项logit模型需要指定其中一类为参照类,k-1个模型分别表示其余各类与参照类相比的结果,回归模型可表示为:
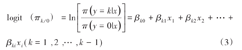
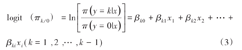
如例1,如果结局变量肥胖(obe1)是三分类变量(1=体重正常,2=超重,3=肥胖),则拟合无序logistic回归的SAS程序:
PROC LOGISTIC data=mnsj1 desc;
CLASS edu(param=reference ref=first);
MODEL obe1(ref="1")=sex edu smo his bp_1/link=glogit;
RUN;



比较图6,图7,图8和图1,图2,图3,区别在于无序logistic回归分别建立了超重(obe1=2)和肥胖(obe1=3)相对于体重正常(obe1=1)的两个logistic回归模型,按式(3),其方程如下:
logit(P2/1)=-0.902 2+0.030 7sex+0.384 1edu2-0.210 9edu3+0.290 8edu4+0.540 8smo-0.167 1 his+0.515 6bp_1;
logit(P3/1)=-1.309 4+0.728 2sex+0.416 4edu2-0.031 0edu3-0.353 8edu4+0.693 1smo- 0.388 7his+0.439 8bp_1。
有序结果的logistic回归(ordinal logistic regression)利用的是累积比数logit模型(cumulative odds model),也称比例优势模型,主要用于处理反应变量为有序分类的情形[1,7]。假设结局变量y为k个等级的有序变量,第k(k=1,2,…,k)类的概率分别为(π1,π2,…,πk),自变量xi(i=1,2,…,i)可以是连续变量、无序或等级变量。回归模型可表示为:
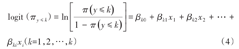
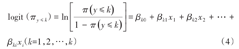
累积比数logit模型应用需要满足比例优势假设(proportional odds assumption)条件,即对于某一自变量xi而言,所有的累积logit都有一个相同的参数估计值,不同累积比数发生比的回归线相互平行。如果这一条件不满足,不能用累积比数logit模型。
具有k个类别的累积比数logit模型也是估计出k-1个模型,但这些模型只有截距不同,各自变量的参数估计值在k-1个模型中是相等的。同样以例1中的结局事件obe1为例,SAS程序是:
PROC LOGISTIC data=mnsj1 desc;
CLASS edu(param=reference ref=first);
MODEL obe1=sex edu smo his bp_1;
RUN;
有序logistic回归与二分类logistic回归的SAS程序是一样的,当结局变量y的分类数大于2时,软件会给出比例优势假设的检验结果(图9)。
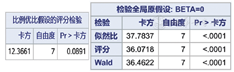

从图9可知,P=0.089 1,不能拒绝"比例性"假设的条件,提示模型满足比例优势假定,可以用累积比数logit模型。其余结果与二分类logistic回归类似(图10,图11,图12)。
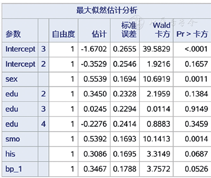

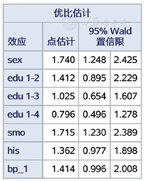

比较图10,图11,图12和图1,图2,图3、图6,图7,图8,区别在于有序logistic回归计算了超重(obe1=2)和肥胖(obe1=3)的截距,但影响因素的参数估计值是唯一的。按式(4),其方程如下:logit(Pk≤2)=-0.352 9+0.553 9sex+0.345 0edu2+0.024 5edu3- 0.227 6edu4+0.539 2smo+0.308 6his+0.346 7bp_1;logit(Pk≤3)=-1.670 2+0.553 9sex+0.345 0edu2+0.024 5edu3- 0.22 76edu4+0.539 2smo+0.308 6his+0.346 7bp_1。
logistic回归是研究一个二分类或多分类反应变量与多个影响因素之间关系的多重回归分析方法。logistic回归的回归系数βi与流行病学研究中的比值比OR是等价的,在医学研究中应用广泛。当自变量为二分类变量时,可以直接纳入logistic回归模型;当自变量为多分类变量时,应采用哑变量的形式纳入模型;当自变量为连续变量或等级变量时,需要验证是否满足线性条件,不满足线性条件时自变量应采取哑变量处理。对于变量的选择,除了从统计学角度通过数量准则进行考察,更要结合专业知识判断变量的重要性;还需要考虑有无必要纳入变量的交互作用;另外,对专业上认为重要但未被选入回归方程的变量,需要查明原因。
本文介绍了三种logistic回归模型,logistic族回归模型还包括条件logistic回归模型(conditional logistic regression model)和相邻优势logistic回归模型(adjacent categorical logistic regression model)。当研究设计为1:m配对设计时,采用条件logistic回归模型,该模型假设自变量在各配比组对结果变量的作用是相同的,即自变量的回归系数与配比组无关,而模型的截距与该组配比因素有关,表示该配比组各自变量为0时的基线风险,对自变量的解释无用,因此,配比设计的logistic回归方程表达为logit (π)=β0+β1x1+β2x2+…+βixi。对不满足比例优势假设条件的有序结果,可以使用相邻优势logistic回归模型,该模型假设相邻等级比较时自变量的回归系数应相等,可通过建立带约束的多分类结果的logistic回归模型来构建,并给定限制条件。
拟合logistic回归模型要对初步构建的模型拟合效果进行评价,影响模型可解释性的原因包括资料的质量、异常值、样本含量太少、纳入的变量太多、应用条件不成立、自变量间存在共线性、自变量保留率极低或极高等。对拟合效果不佳的模型应该进行模型诊断,当存在异常点、多重共线性、空单元格、完全分离或者过离散时,应进行相应处理。最后,需要强调的是,不能盲目进行logistic回归分析,需要结合专业知识,在明确研究目的的基础上,依据科学的数学原理对数据进行分析,实事求是地解释,才能得到相对最佳的回归模型,获得准确又有实际意义的结果。
所有作者均声明不存在利益冲突
1.logistic回归分析适用的结局变量是:
A.分类资料
B.计量资料
C.正态分布资料
D.偏态分布资料
2.logistic回归分析不能用于:
A.预测疾病的发生
B.控制混杂因素
C.估计风险比RR(risk ratio)
D.分析疾病的危险因素
3.不适合做logistic回归分析的是:
A.用身高、胸围预测体重
B.冠心病危险因素筛选
C.吸烟、性别与肺癌发病的关系
D.传染病发病概率的估计
4.以下不能用于logistic回归模型拟合优劣评价的指标是:
A.βi
B. R2
C. HL
D. Pearson χ2
5.logistic回归分析出现空单元格时,处理方法不正确的是:
A.增加样本含量
B.与其相邻类合并
C.采用精确logistic回归
D.采用缺失值填补技术给出估计值



























