
在营养流行病学研究中使用能量控制模型能够从膳食组分摄入量中排除总能量摄入的混杂作用,探究膳食组分摄入与研究结局之间的真实关联。本文介绍了标准多元模型、营养素残差模型、能量分解模型和多元营养素密度模型四种能量控制模型。并以美国国家健康和营养调查研究数据为例,分别采用各种能量控制模型分析饱和脂肪酸摄入量与全因死亡率之间的关联,比较不同能量控制模型的分析结果。分析显示各种能量控制模型结果基本一致,均能较好地控制能量摄入水平的影响。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
在营养流行病学的研究中,能量控制模型广泛地应用于分析膳食组分摄入量与研究结局之间的关联。以营养素为例,营养素的摄入量由膳食摄入总量和膳食构成决定,而反映膳食摄入总量的总能量摄入量受到体型、代谢效率、体力活动等因素影响,可能是研究结局的重要决定因素[1,2,3]。如果在分析中忽略了总能量摄入量的混杂作用,营养素摄入量与研究结局之间的真实关联则可能被掩盖甚至逆转。使用能量控制模型能够模拟"等能量"的代谢实验,排除体型、代谢效率、体力活动等因素引起的外来变异,让研究者更多地关注营养素摄入量中膳食构成贡献的变异与研究结局的特异性关联[4]。在控制了总能量的"等能量模型"(isocaloric model)中进一步考虑其他膳食因素还能模拟膳食干预的作用,探讨营养素之间的替代效应[5],以及判断营养素对研究结局的效应是否独立于其他营养素[1]。此外,能量控制的另外一个重要考量就是在膳食评估中总能量和营养素的测量误差通常具有相同的倾向性,例如研究对象高估或者低估了食物的摄入,则相应的能量摄入也被高估和低估。因此在统计分析中考虑到总能量摄入量的影响将有助于补偿和削弱膳食问卷中测量误差的影响[6,7]。
标准多元模型(standard multivariate model)使用营养素的绝对摄入量与总能量摄入量作为自变量,研究结局作为因变量构成多元回归模型,能够在分析营养素摄入量与研究结局的关联时控制总能量摄入量的影响。在绝大多数情况下,研究的重点并不在于总能量摄入本身与研究结局之间是否有关联,而在于各种营养素对结局的影响。在此模型中,总能量项的效应值表示排除研究关注的营养素之外其他来源的总能量作用,而不能直接解释为总能量摄入量的效应。当研究的营养素摄入量与总能量摄入量具有高度共线性时,将两个变量同时放入模型会明显降低各自的变异,营养素绝对摄入量的生物学意义可能已经发生了改变。因此该模型适用于分析营养素摄入量与总能量摄入量相关性较弱的数据。
该模型可以简化为y=b1 nutrient+b2 calories。此模型中暂未控制其他混杂因素,其中y为结局变量,b1为营养素的效应值,b2为总能量的效应值(如该营养素为供能营养素,例如碳水化合物,b2则代表的是排除碳水化合物以外的其他来源的总能量的效应值,即蛋白质和脂肪所带来的效应值,假设模型中会额外控制酒精摄入或酒精摄入贡献的能量值忽略不计)。
营养素残差模型(nutrient residual model)首先构建以总能量摄入量为自变量,营养素摄入量为因变量的简单线性回归模型,计算经过能量校正的营养素残差。具体操作为nutrient=β1 calories+β0,其中为β1斜率,β0为截距。
根据此公式,则可以得到在某一个体固定能量摄入下其营养素的预测值,而预测值和真实值的差值即为残差。由于残差本身数值有正有负,不好解释,实际分析中通常会用人群中平均能量摄入对应的营养素预测值(固定值)加上每一个人的残差得到每一个人的营养素摄入量(如图1中以饱和脂肪酸和总能量摄入为例计算残差)。从原理上可以看出,残差是与能量摄入无关的变量。因此,该方法可从营养素摄入量的总变异中分离出与总能量摄入量相关的变异,而得到与总能量摄入量无关并能够反映膳食组成的营养素摄入指标。再将营养素残差与总能量摄入量均作为自变量,研究结局作为因变量纳入多元回归模型。该模型中可以观察到总能量摄入量的效应,也可以观察到独立于能量摄入的营养素的效应值。相比于标准多元模型,营养素残差模型明确关注营养素的残差变异而非绝对摄入量,进一步校正总能量摄入量也不会改变其生物学意义,因此能够广泛地应用于各种营养素的分析。
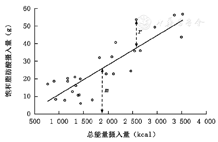

能量校正的营养素摄入量=m+r,其中m是人群中平均能量摄入对应的饱和脂肪酸摄入量预测值,r是回归模型中个体饱和脂肪酸摄入量的残差。1 kcal=4.184 kJ
该模型可以简化为y=b1 nutrient residual+b3 calories。此模型中暂未控制其他混杂因素,其中y为结局变量,b1为营养素的效应值,b3为总能量的效应值。
能量分解模型(energy partition model)将总能量根据来源拆分,并将各部分能量同时作为自变量纳入多元回归模型,适合用于探讨宏量营养素的健康效应。能量分解模型没有控制总能量的作用,并非"等能量模型",因此在解释结果时需要保持谨慎。即使研究关注的营养素所贡献的能量与研究结局有关联,仍然无法确认这种关联是否特异性地来自于研究关注的营养素,还需要对不同来源能量的效应进行比较。
该模型可以简化为y=b4 CalNut+b5 CalOther。此模型中暂未控制其他混杂因素,其中y为结局变量,b4为营养素所贡献能量的效应值,b5为其他营养素贡献能量的效应值。
营养素密度(nutrient density)是营养素摄入量与总能量摄入量的比值,能够反映膳食组分。对于宏量营养素,也可以通过营养素供能比,即该宏量营养素贡献的能量与总能量的比值来表示。单纯使用营养素密度进行分析虽然简便易行,但是能量的测量误差也混入了研究变量中,并且使用营养素摄入量除以总能量摄入量并不一定能够很好地控制总能量的效应[1,8]。多元营养素密度模型(multivariate nutrient density model)同时纳入了营养素密度和总能量摄入量,控制了总能量的混杂作用。改变等量的营养素摄入量理论上对不同体型的个体应该不同,而前三种模型并不能考虑这种差异。而多元营养素密度模型专注于膳食组分与总能量的相对比值,尤其适用于个体间体型差异很大的人群。
该模型可以简化为y=b6 nutrient/calories+b7 calories。此模型中暂未控制其他混杂因素,其中y为结局变量,b6为营养素的效应值,b7为总能量的效应值。
除了以上提到的能量控制模型,在实际研究中还需要考虑除了能量因素以外其他营养素的效应。人们往往关心的是在总能量固定的情况下,增加或减少某一营养素(或食物)所带来的效应,在此情况下,必然有其他营养素(或食物)相应的需要减少或增加来保证能量摄入的平衡。等能量替代模型也得到了越来越多的认可和应用,特别是用于研究宏量营养素之间的替代效应。
本实例使用1999年至2014年美国国家健康和营养调查研究(National Health and Nutrition Examination Survey,NHANES)的18岁及以上参与者第一天访谈调查的24 h膳食回顾数据[9]。排除膳食问卷不合格者、死亡状态未知的参与者、孕妇、总能量摄入量<800 kcal/d或>4 000 kcal/d(1 kcal=4.184 kJ)的男性、总能量摄入<500或>3 500 kcal/d的女性,最终纳入37 639人。死亡结局更新至2015年12月31日,中位随访时间为7.5年,共有4 828人死亡[10]。本实例采用比例风险回归方法,使用各种能量控制模型分析饱和脂肪酸摄入量与全因死亡风险的关联,以及替代其他宏量营养素的效应,并探讨饱和脂肪酸的效应是否独立。所有HR(95%CI)仅校正了年龄、性别、种族因素,并考虑了复杂抽样的权重。数据整理和分析使用SAS 9.4统计软件,SURVEYPHREG过程步MODEL语句代码见表1。

各种能量控制模型函数代码
各种能量控制模型函数代码
| 模型名称 | 模型函数代码 | 模型解释 | |
|---|---|---|---|
| 普通模型 | peryr*mort(0)=sfat age sex race; | 饱和脂肪酸的单独效应,非能量固定 | |
| 标准多元模型 | peryr*mort(0)=sfat kcal age sex race; | 饱和脂肪酸替代其他供能营养素的效应 | |
| 营养素残差模型 | peryr*mort(0)=sfat_r kcal age sex race; | 饱和脂肪酸替代其他供能营养素的效应 | |
| 能量分解模型 | peryr*mort(0)=sfat_e others_e age sex race; | 饱和脂肪酸供能增加,总能量摄入也增加 | |
| 多元营养素密度模型 | peryr*mort(0)=sfat_d kcal age sex race; | 饱和脂肪酸替代其他供能营养素的效应 | |
| 替代碳水化合物 | |||
| 标准多元模型 | peryr*mort(0)=sfat mfat pfat prot kcal age sex race; | 饱和脂肪酸等能量替代碳水化合物的效应 | |
| 营养素残差模型 | peryr*mort(0)=sfat_r mfat_r pfat_r prot_r kcal age sex race; | 饱和脂肪酸等能量替代碳水化合物的效应 | |
| 多元营养素密度模型 | peryr*mort(0)=sfat_d mfat_d pfat_d prot_d kcal age sex race; | 饱和脂肪酸等能量替代碳水化合物的效应 | |
| 替代多不饱和脂肪酸 | |||
| 标准多元模型 | peryr*mort(0)=sfat mfat tfat kcal age sex race; | 饱和脂肪酸替代多不饱和脂肪酸的效应 | |
| 营养素残差模型 | peryr*mort(0)=sfat_rt mfat_rt tfat_r kcal age sex race; | 饱和脂肪酸替代多不饱和脂肪酸的效应 | |
| 多元营养素密度模型 | peryr*mort(0)=sfat_d mfat_d tfat_d kcal age sex race; | 饱和脂肪酸替代多不饱和脂肪酸的效应 | |
| 校正其他脂肪酸 | |||
| 标准多元模型 | peryr*mort(0)=sfat mfat pfat kcal age sex race; | 饱和脂肪酸等能量替代蛋白质和碳水化合物的效应 | |
| 营养素残差模型 | peryr*mort(0)=sfat_r mfat_r pfat_r kcal age sex race; | 饱和脂肪酸等能量替代蛋白质和碳水化合物的效应 | |
| 多元营养素密度模型 | peryr*mort(0)=sfat_d mfat_d pfat_d kcal age sex race; | 饱和脂肪酸等能量替代蛋白质和碳水化合物的效应 | |
注:模型函数中变量名的含义分别是:age:年龄,sex:性别,race:种族,kcal:总能量摄入量,prot:蛋白质摄入量,tfat:总脂肪摄入量,sfat:饱和脂肪酸摄入量,others_e:除饱和脂肪酸外其他来源的能量,mfat:单不饱和脂肪酸摄入量,pfat:多不饱和脂肪酸摄入量,mort:死亡状态,peryr:随访人年数。_r表示能量校正的残差,_rt表示总脂肪校正的残差,_e表示该营养素贡献的能量,_d表示营养素密度
能量校正降低了营养素摄入量与总能量摄入量的相关性。能量校正的饱和脂肪酸残差和饱和脂肪酸供能比均与饱和脂肪酸的绝对摄入量存在较强的正相关(r分别为0.66和0.71,P值均<0.001),饱和脂肪酸的绝对摄入量与总能量摄入量呈正相关(r=0.75,P<0.001),能量校正的饱和脂肪酸残差和饱和脂肪酸供能比与总能量摄入量之间没有相关性(r=0.001,P>0.99)或较弱相关性(r=0.13,P<0.001)。饱和脂肪酸摄入量与全因死亡风险关联的分析结果见表2。在未考虑能量摄入水平时,分析结果显示饱和脂肪酸摄入量每增加22 g(对应约200 kcal的能量摄入,即按照成人2 000 kcal的能量摄入,22 g饱和脂肪酸提供约10%的能量)与全因死亡率降低显著相关。而使用标准多元模型后,每增加22 g饱和脂肪酸摄入,全因死亡风险增加15%。营养素残差模型中饱和脂肪酸的分析结果与标准多元模型的结果完全相同,能量项的结果也和总能量的单独效应一致(HR=0.96,95%CI:0.95~0.97)。能量分解模型显示饱和脂肪酸提供的能量每增加200 kcal能够增加8%的全因死亡风险,在此模型中等量其他来源的能量摄入则与全因死亡风险降低相关(HR=0.94,95%CI:0.93~0.96)。多元营养素密度模型也提示饱和脂肪酸供能比每增加10%,全因死亡风险将升高13%。
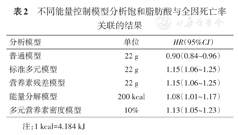
不同能量控制模型分析饱和脂肪酸与全因死亡率关联的结果
不同能量控制模型分析饱和脂肪酸与全因死亡率关联的结果
| 分析模型 | 单位 | HR(95%CI) |
|---|---|---|
| 普通模型 | 22 g | 0.90(0.84~0.96) |
| 标准多元模型 | 22 g | 1.15(1.06~1.25) |
| 营养素残差模型 | 22 g | 1.15(1.06~1.25) |
| 能量分解模型 | 200 kcal | 1.08(1.01~1.17) |
| 多元营养素密度模型 | 10% | 1.13(1.05~1.23) |
注:1 kcal=4.184 kJ
饱和脂肪酸对全因死亡风险的营养素替代模型结果见表3。以标准多元模型结果为例,每22 g饱和脂肪酸替代等能量的碳水化合物,全因死亡率增加15%,替代等量多不饱和脂肪酸则将增加28%的全因死亡风险。在校正单不饱和脂肪酸和多不饱和脂肪酸两类脂肪的影响后,饱和脂肪酸仍然显示出对全因死亡风险的独立效应。

饱和脂肪酸对全因死亡风险的营养素替代模型结果[HR(95%CI)]
饱和脂肪酸对全因死亡风险的营养素替代模型结果[HR(95%CI)]
| 分析模型 | 单位 | 替代碳水化合物 | 替代多不饱和脂肪酸 | 校正其他类型脂肪酸 |
|---|---|---|---|---|
| 标准多元模型 | 22 g | 1.15 (1.02~1.28) | 1.28 (1.11~1.47) | 1.13 (1.01~1.26) |
| 营养素残差模型 | 22 g | 1.15 (1.02~1.28) | 1.28 (1.11~1.47) | 1.13 (1.01~1.26) |
| 多元营养素密度模型 | 10% | 1.14 (1.03~1.27) | 1.25 (1.09~1.43) | 1.13 (1.02~1.26) |
实例分析在考虑能量摄入水平后,不同模型中饱和脂肪酸的摄入量均显示与全因死亡风险增加有关。这可能是未考虑能量时,体力活动和疾病状态等混杂因素混淆了饱和脂肪酸的效应。比如运动量大的人吃得食物更多,饱和脂肪摄入也随之增多,但这些人的死亡风险较低;而死亡风险较高的患者群体吃的食物则通常较少,饱和脂肪摄入水平也更低一些。
各种能量控制模型的分析结果具有互通之处。控制了总能量的营养素残差模型与标准多元模型的结论一致。而在能量分解模型中,饱和脂肪酸贡献的能量与其他来源的能量之间效应的差值,同样与标准多元模型和营养素残差模型基本一致,也能表示饱和脂肪酸独立于总能量的作用。尽管营养素密度与营养素残差的计算方法并不相同,但是两个指标通常具有较高的相关性(本例中r值为0.92),分析结果也基本一致。
尽管四种能量控制模型在实例分析中表现相似,但各自的优缺点仍然需要得到注意。标准多元模型结构简单,操作方便,不过在此模型中无法观察到总能量摄入量的完整效应,并且在营养素绝对摄入量与总能量摄入量强相关时,营养素绝对摄入量的变异程度会大大降低,失去原有的生物学意义。虽然计算营养素残差的操作步骤略为复杂,但是营养素残差模型适用范围广泛,模型中的能量项也能够反映总能量的完整效应。使用能量分解模型时需要计算各宏量营养素贡献的能量,因此不适合研究不供能的微量营养素;并且由于模型中没有控制总能量,在分析部分膳食因素时实际上与未固定能量的普通模型相同,并不适合分析营养素的替代作用和独立效应。而相比其他模型,营养素密度作为相对数指标在应用于能量摄入水平相差较大的人群时更具优势。但在使用多无营养素密度模型时也需要注意到,如果营养素摄入量变异很小,营养素密度则可能是人为制造的一个与总能量摄入量呈高度负相关的变量[1]。例如,如果在一个研究中,总能量摄入与结局之间呈正相关关系,而营养素本身并无作用,那么营养素密度则可能与结局之间呈现负相关关系。
分析营养素替代作用和独立效应时,三种"等能量模型"的分析结果基本一致。但相比控制总脂肪的模型,替代多不饱和脂肪酸的模型更加强调比较不同类型的脂肪酸的作用。而在校正其他类型脂肪酸的模型中,如果模型中有两种脂肪酸的效应有统计学意义,这将比仅仅控制总能量的模型更能说明不同类型脂肪酸的独立效应。并且在此模型中,饱和脂肪酸与多不饱和脂肪酸效应的差值与两者之间的替代效应基本一致。
现实中膳食问卷调查测量的能量不够精确,这使得能量校正模型受到了一些挑战[11]。但是作为"金标准"的双标水法成本高昂、操作复杂,难以在大规模研究中实施。影响能量的体力活动和代谢效率等因素缺乏简单、精确的测量方法,并且使用体重和体力活动校正等方法仍有待于更多研究的探讨和验证,目前在营养流行病学研究中使用能量校正模型仍不失为一种有效的办法[8]。
应用能量控制模型的目的主要是为了在研究营养素的健康效应时尽可能排除能量摄入水平的混杂作用,厘清统计学关联是否特异性地来自于营养素摄入量的差异。研究者在选择和使用这些模型时不仅需要在选择分析方法时综合考虑研究人群的特点和营养素的特性,还需要结合生物学机制对分析模型和统计结果的意义有更深入的理解。
所有作者均声明不存在利益冲突
1.为什么需要使用能量控制模型:
A.能量摄入水平可能是疾病的重要决定因素
B.营养素摄入量与总能量摄入量呈正相关
C.总能量摄入量受到体型、代谢效率、体力活动等因素影响
D.营养素和总能量的测量误差具有相同的倾向性
E.以上原因都是
2.以下描述的不正确的是:
A.营养素残差与总能量在理论上没有相关性
B.能量校正的营养素摄入量等于人群中平均能量摄入对应的营养素摄入量预测值减去回归模型中个体营养素摄入量的残差
C.营养素残差模型中能够观察到总能量的效应
D.能量分解模型不适用于非供能营养素
E.等能量替代模型适合分析供能营养素之间的关系
3.下列哪种能量控制模型不是"等能量模型":
A.标准多元模型
B.营养素残差模型
C.能量分解模型
D.多元营养素密度模型
E.营养素替代模型
4.分析碳水化合物等能量替代总脂肪的模型中需要纳入哪些变量:
A.碳水化合物能量
B.碳水化合物总脂肪能量
C.碳水化合物蛋白质能量
D.碳水化合物蛋白质总脂肪能量
E.碳水化合物蛋白质
5.为什么能量分解模型不适合用于分析营养素替代作用和独立效应:
A.只适用于宏量营养素的分析
B.模型中无法观察总能量的完整效应
C.等量宏量营养素贡献的能量不相等
D.模型中没有控制总能量
E.无法校正其他膳食因素



























