Joinpoint回归模型有线性模型（y=xb）和对数线性模型（ln y=xb）两种，如果因变量服从正态分布（或近似正态分布）且数据样本量较大（通常大于100）时选择线性模型；如果因变量服从指数分布或泊松分布，则宜选用对数线性模型。分析以人群为基础的肿瘤发病率和死亡率趋势时一般选择对数线性模型。假设有一组观测值y表示肿瘤发病率，x表示发病年份，n表示研究的时间跨度，以（x₁，y₁）, …（x_n，y_n）表示，其中x₁≤…≤x_n，对数线性模型的回归方程式为：

E y | x = e β 0 + β 1 x + δ 1 ( x - τ 1 ) + + … + δ k ( x - τ k ) +

式中，e为自然底数，k表示转折点的个数，τ_k表示未知的转折点，β₀为不变参数，β₁为回归系数，δ_k表示第k段分段函数的回归系数。当（x-τ_k）>0时，(x-τ_k)⁺)=x-τ_k，否则(x-τ_k)⁺)=0。

网格搜索法（grid search method, GSM）是Joinpoint默认采用的建模方法。GSM是将研究数据划分为网格，每个网格交点对应一个规划方案，然后在设定的区间内用固定步长逐点计算对应方程的性能指标，以确定最优函数^{［2, 3］}。简言之，Joinpoint模型通过GSM法建立所有可能存在的区间分段函数连接点（即Joinpoint点），并计算每种可能的情况下所对应的误差平方和（sum of squares errors，SSE）和均方差（mean squared errors, MSE）, 选择MSE最小的网格点为分段函数连接点，并根据选定的连接点和区间函数拟合β₀、β₁、δ₁、... δ_k等方程参数。除了GSM法外，Joinpoint软件早期版本中还提供了Hudson′s 法的备选项，现已取消。

Monte Carlo置换检验（permutation test）是Joinpoint软件默认的模型优选方法。建模之前，需要先设定连接点k的数量范围k_ϵ(MIN, MAX), MIN表示最少连接点数，通常情况下可设为0；MAX表示最多连接点数。每一次置换检验会检验原假设H₀：设连接点数量K=K_a以及备选假设H₁：连接点数量k=k_b。置换检验从k_a=MIN和k_b=MAX开始，如果拒绝H₀，则设k=k_a+1后再进行检验；如果不拒绝H₀，则设k=k_b-1后再次进行检验，直到k_a=k_b, 即k=k_a=k_b就是置换检验优选出的连接点数，其对应的模型即为最优模型^［4］。因为置换检验相对耗时，为了兼顾运算速度和结果的稳定性，官方推荐和系统默认的置换检验的次数为4 500次，因为涉及多重检验，所以采用Bonferroni法对统计学显著水平进行校正。除Monte Carlo置换检验外，软件还提供了贝叶斯信息准则（bayesian information criterion，BIC）、校正贝叶斯信息准则（modified bayesian information criterion，MBIC）及相关衍生方法进行优选模型的筛选，但主要面向特殊需求的高级用户使用。

年度变化百分比（annual percent change, APC）和平均年度变化百分比（average annual percent change, AAPC）及95%CI是Joinpoint模型主要结果指标。顾名思义APC为因变量平均每年变化的百分比。例如对数线性模型ln(y)=β₀+β₁x, 其中y表示发病率，x表示发病年份，则拟合模型APC计算公式可推算为：

A P C = y x + 1 - y x y x × 100 = ( e β 1 - 1 ) × 100

100（1-α）%可信区间下限和上限分别为：

A P C L ( α ) = 100 ( e β 1 - s × t d - 1 1 - α / 2 - 1 )

A P C U ( α ) = 100 ( e β 1 + s × t d - 1 1 - α / 2 - 1 )

式中，β₁为回归系数，s为β₁的标准误，d为自由度，t_d（q）是自由度d的 t分布对应第q百分位数（如95%）的数值。

APC用于评价分段函数各独立区间的内部趋势，或者连接点数量为0的全局趋势，如果要综合评价包含多个区间的全局平均变化趋势时就需要用AAPC。AAPC的参数计算方法是通过分段区间的跨度宽度w对各区间的回归系数进行加权计算而来，其公式为：

A A P C = e ∑ w i β i / ∑ w i - 1 × 100

100（1-α）%可信区级下限和上限分别为：

A A P C L ( α ) = e x p l n ( ( A A P C / 100 ) + 1 ) - Z 1 - α / 2 ∑ w ˜ i 2 σ ˜ i 2 - 1

A A P C U ( α ) = e x p l n A A P C / 100 + 1 + Z 1 - α / 2 ∑ w ˜ i 2 σ ˜ i 2 - 1

式中，w_i为每个分段函数的区间跨度宽度（即区间所包括的年度数），β_i为每个区间对应的回归系数，w˜i=wi/∑wi为正态加权系数，σ˜i2为β_i的方差，Z_α为正态分布下第α百分位数的对应值。

下载Joinpoint软件需登录美国国立癌症研究所网站（https://surveillance.cancer.gov/joinpoint/download），注册提交申请信息后可下载并安装至本地电脑免费使用，软件定期更新，目前官方最新版本为Joinpoint 4.8.0.1（2020年4月发布）。

Joinpoint软件支持的可读入文件格式仅包括ASCII的后缀“.txt”文本和Excel spreadsheet的“.CSV”文件格式。读入数据可以通过SAS、Stata、SPSS、Excel或其他软件（如SEER*Stat）转换或导出。数据准备完成后通过Joinpoint软件打开，根据研究数据的不同类型选定因变量、自变量和分组变量读入软件中。因变量支持两种模式：一是提供已计算好的粗率、标化率、标准误等结果指标；二是提供各年龄组对应的病例频数、人口数和标化人口数等，由软件运行计算结果，再进行趋势分析。

一般情况下主要设置3个参数：（1）是否选用对数线性模型（log transformation），如何选择前文已阐述；（2）方差齐性的误差选项（heteroscedastic error option）：假定研究数据方差稳定的情况下，可以选择“恒方差［constant variance（homoscedastic）］”；如果考虑方差变异较大时可选择“标准误［standard error（provided）］”或者“泊松（poisson variance）”。选择“标准误”的话需要提供或者计算标准误，选“泊松”的话仅支持因变量类型为频数和人口数的模式。粗率标准误的计算公式如下：

S E c r u d e = c o u n t p o p u l a t i o n × 100 000

假定事件发生数（count）服从泊松分布，各年龄组i从年龄x到y岁，则标化发病率的标准误计算公式为：

S E A S R = ∑ i = x y s t d p o p i ∑ i = x y s t d p o p i 2 × c o u n t i p o p u l a t i o n i 2 × 100 000

式中stdpop_i为i年龄组标准人口，count_i为i年龄组事件频数，population_i为对应人口数。（3）连接点数量：连接点的数量与研究数据的时间跨度的宽度（观测值数量）有关，系统默认最小为0，最大为5，用户可根据需求自行定义。但连接点过多的话运算相当耗时，因此软件推荐的观测值数量与系统默认最大连接数量有如下的对应关系：观测值数量分别为0~6、7~11、12~16、17~21、22~26、≥27时，默认最大连接点数量分别为0、1、2、3、4、5。除上述参数外，软件还支持“模型选择方法（Model select Method）”“AAPC计算范围设定”“APC/AAPC 可信区间算法”“自相关误差选项（Auto Errors Options）”等参数选择，供有特殊需要的高级用户，具体需求可参照软件说明，一般情况下选择默认设置即可。

示例数据库类型为txt格式，采用Joinpoint软件打开后可见，库中包含性别、诊断年份、年龄组别、年龄组发病、年龄组发病例数、年龄组人口数和年龄组标准人口数。数据读入环节因变量类型选择“Calculated From Data File”，根据软件的需要依次选择频数变量（Count Variable)、人口变量（Population Variable)、调整/标化变量（Adjustment Variable）和标准人口变量（Standard Variable)，并设定自变量（Independent Variable）和分组变量（By Variables, 可选项），在系统默认的对数线性模型选择方差误差（Heteroscedastic Errors Option）选项为“Standard Error（Caculated）”即可运行（图1）。

点击查看大图

图1

1993—2003年美国SEER结直肠癌发病数据库以“发病例数+人口数”为读入模式的Joinpoint变量选择与参数设置

点击查看大图

图1

1993—2003年美国SEER结直肠癌发病数据库以“发病例数+人口数”为读入模式的Joinpoint变量选择与参数设置

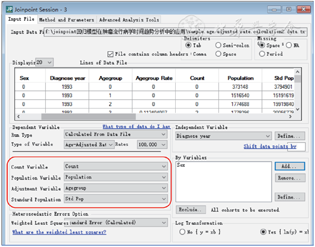
运算完毕后呈现结果如图2所示，左侧部分为模型的选择结果，本示例中0、1、2分别表示分组变量中的“男女合计”“男性”和“女性”，可以选择查看不同连接点数对应的模型，其中加星号的是系统优选推荐的模型；右侧主体窗口有“Graph”“Data”“Model Estimates”“Trend”和“Model Selection”五个选项，分别对应模型拟合的拐点/曲线图、计算/拟合的应变量数据、选定模型的参数指标、APC/AAPC和95%CI趋势指标，以及模型优选的置换检验情况。

点击查看大图

图2

1993—2003年美国SEER结直肠癌发病数据Joinpiont 回归分析趋势结果

点击查看大图

图2

1993—2003年美国SEER结直肠癌发病数据Joinpiont 回归分析趋势结果

以男女合计的发病率变化趋势结果为例，1993—2013年间SEER结直肠癌标化发病率分别在1995、1998和2008年出现三个拐点（连接点），对应4个区间的APC（95%CI）分别为APC_1993-1995=-2.55(95%CI:-5.91~0.94,P=0.133)、APC_1995-1998=1.92(95%CI:-1.52~5.48,P=0.245)、APC_1998-2008=-2.37(95%CI:-2.67~-2.07,P<0.001)、APC_2008-2013=-2.14(95%CI:-2.71~-1.56,P<0.001)]，全局AAPC_1993-2013=-3.87(95%CI:-4.64~-3.10,P<0.001)]。全局AAPC结果表明，1993—2013年间美国SEER结直肠癌发病率平均每年下降3.87%。最终优选的拟合模型回归方程为：

y = e 55.423865 - 0.025782 x + 0.044800 x - 1995 + - 0.043007 ( x - 1998 ) + - 0.015481 ( x - 2008 ) +

式中y为发病率，x为诊断年份，模型参数均可在Model Estimates选项中查阅。

将已下载的示例数据库作适当演算，生成以标化发病率作为因变量的读入数据类型，选择“恒方差”误差选项，参数设置如图3所示，即可运行。对比因变量为“发病例数+人口数”模式和因变量为“标化发病率”模式的分析结果，即“恒方差”和“标准误”不同误差选项的运行结果可以发现，两个结果中连接点的数量与位置完全一致，APC/AAPC及95%CI大小差异微小，提示研究数据的误差变异较小时，两种计算模式均可选择。见图4。

点击查看大图

图3

1993—2003年美国SEER结直肠癌发病数据库以“标化发病率”为读入模式的Joinpoint变量选择与参数设置

点击查看大图

图3

1993—2003年美国SEER结直肠癌发病数据库以“标化发病率”为读入模式的Joinpoint变量选择与参数设置

点击查看大图

图4

1993—2003年美国SEER结直肠癌发病趋势分析采用“标准误”和“恒方差”选项对应的APC/AAPC结果差异

点击查看大图

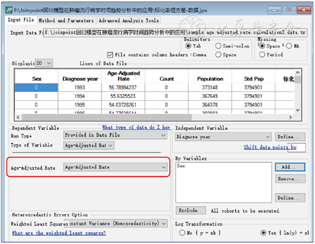
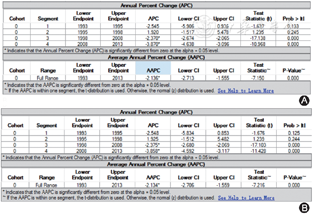
A: 因变量为“发病例数+人口数”的“标准误”误差选项； B:因变量为“标化发病率”的“恒方差”选项

图4

1993—2003年美国SEER结直肠癌发病趋势分析采用“标准误”和“恒方差”选项对应的APC/AAPC结果差异