
传统比例风险模型通常只关注一种主要结局事件,而医学研究中的观察终点往往并不唯一。将主要结局事件之外的其他结局事件记为删失的分析方法,理论上会导致主要结局事件发生概率的有偏估计。传统竞争风险模型虽然能调整其他结局事件对主要结局事件发生风险的竞争影响,但无法直接比较个体发生不同结局事件之间的风险差异。多状态竞争风险模型为此提供了相对合适的解决方案。本文以前列腺癌患者长期随访数据集为例,分别构建了以前列腺癌死亡和其他原因死亡为主要结局事件的传统比例风险模型和传统竞争风险模型,以及同时考虑前列腺癌死亡和其他原因死亡的多状态竞争风险模型。通过比较三种模型在生存数据分析的优缺点,明确多状态竞争风险模型的临床应用价值,从而更好地指导包含竞争结局事件的生存数据分析。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
传统生存分析通常只关心一个主要结局事件(研究者感兴趣的结局),而医学研究中的观察终点往往并不唯一(出现不感兴趣的其他结局)。如癌症患者在观察期内可能死于癌症,也可能死于其他疾病,即出现竞争风险(competing risks)。对竞争风险的忽视,往往会导致个体生存率的有偏估计。同时,在临床实践中,由于仅关注主要结局事件(如降低癌症复发、转移或死亡),忽视竞争结局事件风险(由于过度强调治疗,而忽视癌症治疗本身带来的副反应增加的竞争结局事件发生风险增加),最终癌症死亡风险可能降低,但同时可能会增加癌症治疗副反应带来的竞争结局事件(如心血管死亡)发生风险[1, 2]。传统竞争风险模型虽然能调整其他结局事件对主要结局事件发生风险的竞争影响,但无法直接比较多个结局事件之间的风险差异。此时多状态竞争风险模型将提供更为有效的分析方案。本研究以前列腺癌患者死亡竞争结局事件风险数据集为例,分别构建不同的生存分析模型,并分析比较不同模型的合理性及局限性,为包含多结局事件的生存数据分析提供参考。
传统比例风险模型(proportional hazard model),或称无病生存风险(event-free survival,EFS)模型,最早由Cox于1972年提出[3]。该模型的基本假设是:不论基线风险如何,在任何时间点上,存在某一暴露的个体相对不存在该暴露的个体发生事件的风险是恒定的,故该模型称为比例风险模型。模型构建时,未观察到结局事件记为0,观察到结局事件记为1。分析方法上,单因素分析时采用log-rank检验比较暴露组和非暴露组的Kaplan-Meier生存曲线是否存在差异[4];多因素分析时采用传统Cox比例风险回归模型比较调整其他混杂因素影响后暴露组和非暴露组主要结局事件的发生风险是否存在差异。
传统竞争风险模型(competing risk model),又称累积发生函数(cumulative incidence function,CIF)模型,最早由Fine和Gray于1999年提出[5]。该模型的基本假设是:在比例风险假设前提下,个体发生主要结局事件与其他结局事件的风险相互独立,也即发生主要结局事件者,将不再发生其他结局事件,因此主要结局与其他结局之间存在竞争关系。模型构建时,未观察到任何结局事件记为0,观察到的结局事件(如癌症死亡和其他原因死亡)依次记为1、2、3或更多。但在计算主要结局事件(如结局事件标记为1)累积发生风险时,发生其他结局事件(如结局事件标记为2或其他)的患者将不被计入初始风险人群(在传统比例风险模型中,该部分人群被记为删失数据,该处理是传统比例风险模型与传统竞争风险模型的本质区别所在),由此分别计算不同结局事件各自的累积发生函数,因此,传统竞争风险模型又称为原因别风险(cause-specific risk,CSR)模型。分析方法上,单因素分析时采用Gray′s检验比较暴露组和非暴露组的Nelson-Aalen累积风险生存曲线是否存在差异;多因素分析时采用竞争风险模型比较调整其他混杂因素并控制竞争风险影响后暴露组和非暴露组主要结局事件的累积发生风险是否存在差异[5, 6, 7]。
多状态竞争风险模型(multi-state competing risk model),又简称多状态模型(multi-state model,MSM),最早由Andersen于2002年提出[8, 9]。该模型的基本假设是:在比例风险假设前提下,个体可以从不同状态(如早期癌和晚期癌)进入模型,也可以发展为多种不同状态或结局事件(如复发、转移、治疗后好转及死亡);除结局事件为吸收状态(absorbing state,如死亡)无法再发展为其他状态,其他结局事件(或称中间状态)之间允许相互进展,也即不同结局事件或不同状态之间既可以同时存在(如同时存在两种吸收状态:癌症死亡和其他原因死亡),也可以相互进展(如复发到死亡、转移到死亡,复发到转移等),后者是传统竞争风险模型与多状态竞争风险模型的本质区别[6,8, 9, 10]。模型构建时,将不同的结局事件或状态(如健康存活、复发、转移、治疗后好转及死亡)分别记为1、2、3或更多,根据不同状态之间的进展方向定义状态进展变量[如从健康存活(状态1)到复发(状态2)定义为进展方向1、从健康存活(状态1)到转移(状态3)定义为进展方向2、从复发(状态2)到转移(状态3)定义为进展方向3,等],并重新构建数据集,即在原有数据集基础上分别增加起始状态、终末状态,和状态进展变量三个变量信息。分析方法上,以新数据集构建多变量的生存分析模型,除纳入前述的协变量外,同时纳入疾病状态进展变量及其与协变量的交互项。如果交互项存在统计学意义,说明该协变量特定亚组人群发生不同结局事件的风险差异存在统计学意义[6,8, 9, 10, 11]。由于结局变量由多状态组成,结局变量的分布类型检验是多状态竞争风险模型目前相对难以评价的问题。当多种结局状态仅由相互独立的吸收状态组成时,结局变量符合基本的多项分布;当多种结局状态之间存在相互进展时,结局变量的分布类型尚无法直接检验。
上述三种生存数据分析模型的共同点是基本假设均为比例风险假设。如比例风险假设不满足,则需要在上述模型基础上通过增加时间依赖变量等方法来进行调整和完善。实际分析时,应根据研究目的选择合适的模型,当比较多种结局风险差异时,优先选择多状态竞争风险模型。三种模型的优缺点比较见表1。

常见3种生存分析模型的特征比较
常见3种生存分析模型的特征比较
| 特征 | 传统比例风险模型 | 传统竞争风险模型 | 多状态竞争风险模型 |
|---|---|---|---|
| 基本原理 | 比例风险假设 | 比例风险假设+竞争风险假设 | 比例风险假设+多状态进展假设 |
| R程序包 | survival | cmprsk | mstate |
| 优点 | 结果简便易读 | 能分析2个或更多结局事件的生存数据 | 能同时分析并比较2个或更多结局事件的发生风险差异 |
| 缺点 | 无法处理2个或更多结局事件的生存数据 | 假定多个结局事件的发生风险相互独立,可分别独立计算原因别累积发生函数,但无法直接比较不同结局事件的风险差异 | 当多种结局事件之间存在相互进展时,结局变量的分布类型尚无法直接检验 |
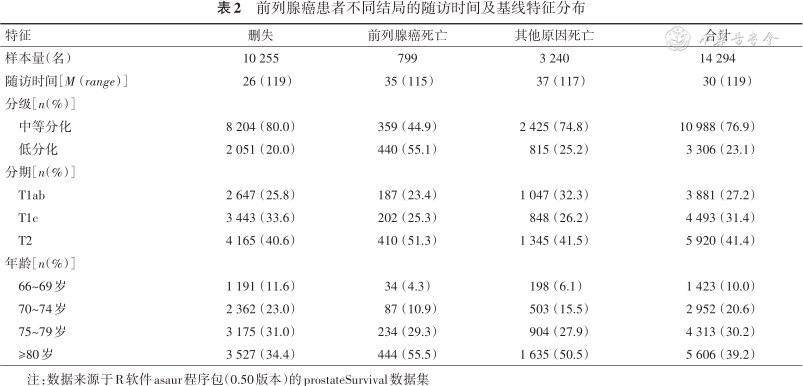
采用的数据集来源于R软件asaur程序包(0.50版本)的prostateSurvival数据集。该数据集是Lu-Yao等[12]于1992—2002年收集的14 294名诊断时分期为T1或T2期、且诊断后6个月内没有进行手术或放疗的癌症患者的生存数据集。该数据集收集了前列腺癌患者诊断时的肿瘤分级(好/差)、分期(T1ab/T1c/T2)和年龄分组(66~69、70~74、75~79、≥80岁)信息,同时收集了患者从诊断到死亡的随访时间,并将死因区分为前列腺死亡和其他原因死亡。所有患者平均随访38.96个月,研究期间,共计799人发生前列腺癌死亡,3 240人发生其他原因死亡,见表2。
前列腺癌患者不同结局的随访时间及基线特征分布
前列腺癌患者不同结局的随访时间及基线特征分布
| 特征 | 删失 | 前列腺癌死亡 | 其他原因死亡 | 合计 |
|---|---|---|---|---|
| 样本量(名) | 10 255 | 799 | 3 240 | 14 294 |
| 随访时间[M(range)] | 26(119) | 35(115) | 37(117) | 30(119) |
| 分级[n(%)] | ||||
中等分化 | 8 204(80.0) | 359(44.9) | 2 425(74.8) | 10 988(76.9) |
低分化 | 2 051(20.0) | 440(55.1) | 815(25.2) | 3 306(23.1) |
| 分期[n(%)] | ||||
T1ab | 2 647(25.8) | 187(23.4) | 1 047(32.3) | 3 881(27.2) |
T1c | 3 443(33.6) | 202(25.3) | 848(26.2) | 4 493(31.4) |
T2 | 4 165(40.6) | 410(51.3) | 1 345(41.5) | 5 920(41.4) |
| 年龄[n(%)] | ||||
66~69岁 | 1 191(11.6) | 34(4.3) | 198(6.1) | 1 423(10.0) |
70~74岁 | 2 362(23.0) | 87(10.9) | 503(15.5) | 2 952(20.6) |
75~79岁 | 3 175(31.0) | 234(29.3) | 904(27.9) | 4 313(30.2) |
≥80岁 | 3 527(34.4) | 444(55.5) | 1 635(50.5) | 5 606(39.2) |
注:数据来源于R软件asaur程序包(0.50版本)的prostateSurvival数据集
传统比例风险模型构建时,以前列腺癌死亡为观察结局时,将删失和其他原因死亡合并为删失;同理,以其他原因死亡为观察结局时,将删失和前列腺癌死亡合并为删失。同时,可以将前列腺癌死亡和其他原因死亡合并计算单纯死亡的影响因素,但与后续传统竞争风险模型和多阶段竞争风险模型探讨死因特异性影响因素的研究目的不一致,故本实例分析时不设计相关分析。传统竞争风险模型构建时,为明确原因别累积发病风险的差异,分别以前列腺癌死亡和其他原因死亡为主要结局构建竞争风险模型。多状态竞争风险模型中,前列腺癌死亡和其他原因死亡均设为吸收状态,同时纳入模型。为便于传统竞争风险模型与多状态竞争风险模型进行比较,多状态竞争风险模型仅设计2个疾病进展方向:从诊断到前列腺癌死亡(疾病进展方向1,参考疾病进展方向)和从诊断到其他原因死亡(疾病进展方向2,考察进展方向)。当采用复杂多状态竞争风险模型时,该实例可以同时设计其他状态进展方向:如从T1期前列腺癌到前列腺癌死亡(或其他原因死亡),从T2期前列腺癌到前列腺癌死亡(或其他原因死亡)等。同时分别纳入前列腺癌诊断分级、分期及年龄三个变量与状态进展变量的交互项,以分别探讨三个变量不同暴露状态下发生前列腺癌和其他原因死亡的风险差异是否存在统计学意义。
传统比例风险模型、传统竞争风险模型及多状态竞争风险模型分别采用R软件(4.0.3版本)的survival程序包(3.2-7版本)、cmprsk程序包(2.2-10版本)、mstate程序包(0.3.1版本)完成,代码见附件1。多因素分析时不同协变量与结局发病风险关联强度采用HR(95%CI)值表示。所有统计分析均采用双侧检验,检验水准α=0.05。
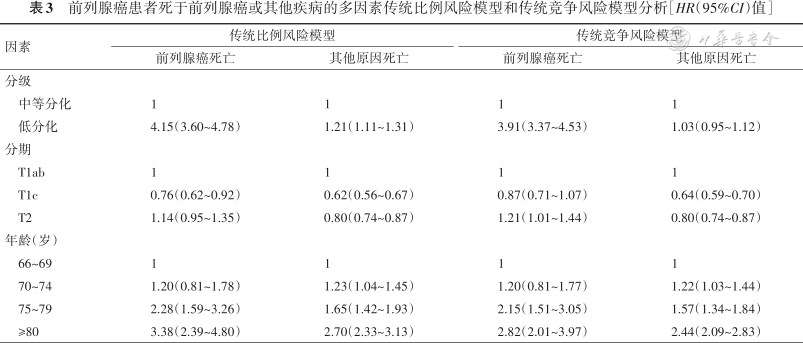
1.传统比例风险模型和传统竞争风险模型的多因素分析:不论是传统比例风险模型,还是传统竞争风险模型,前列腺癌患者诊断时的分级、分期和年龄都是前列腺癌死亡和其他原因死亡的独立影响因素。但传统比例风险模型和传统竞争风险模型的多因素分析的差异体现在:传统比例风险模型下,与T1ab期相比,T1c期的前列腺癌患者死亡风险显著降低[HR:0.76(95%CI:0.62~0.92)],T2期前列腺癌患者死亡风险差异没有统计学意义[HR:1.14(95%CI:0.95~1.35)];但在传统竞争风险模型下,与T1ab期相比,T1c期前列腺癌患者死亡风险没有显著差异[HR:0.87(95%CI:0.71~1.07)],T2期前列腺癌患者死亡风险显著增加[HR:1.21(95%CI:1.01~1.44)]。同样,传统比例风险模型下,与中等分化患者相比,低分化患者因其他原因造成的死亡风险显著增加[HR:1.21(95%CI:1.11~1.31)];但在传统竞争风险模型下,低分化与中等分化患者中因其他原因造成的死亡风险差异没有统计学意义[HR:1.03(95%CI:0.95~1.12)]。见表3。
前列腺癌患者死于前列腺癌或其他疾病的多因素传统比例风险模型和传统竞争风险模型分析[HR(95%CI)值]
前列腺癌患者死于前列腺癌或其他疾病的多因素传统比例风险模型和传统竞争风险模型分析[HR(95%CI)值]
| 因素 | 传统比例风险模型 | 传统竞争风险模型 | ||
|---|---|---|---|---|
| 前列腺癌死亡 | 其他原因死亡 | 前列腺癌死亡 | 其他原因死亡 | |
| 分级 | ||||
中等分化 | 1 | 1 | 1 | 1 |
低分化 | 4.15(3.60~4.78) | 1.21(1.11~1.31) | 3.91(3.37~4.53) | 1.03(0.95~1.12) |
| 分期 | ||||
T1ab | 1 | 1 | 1 | 1 |
T1c | 0.76(0.62~0.92) | 0.62(0.56~0.67) | 0.87(0.71~1.07) | 0.64(0.59~0.70) |
T2 | 1.14(0.95~1.35) | 0.80(0.74~0.87) | 1.21(1.01~1.44) | 0.80(0.74~0.87) |
| 年龄(岁) | ||||
66~69 | 1 | 1 | 1 | 1 |
70~74 | 1.20(0.81~1.78) | 1.23(1.04~1.45) | 1.20(0.81~1.77) | 1.22(1.03~1.44) |
75~79 | 2.28(1.59~3.26) | 1.65(1.42~1.93) | 2.15(1.51~3.05) | 1.57(1.34~1.84) |
≥80 | 3.38(2.39~4.80) | 2.70(2.33~3.13) | 2.82(2.01~3.97) | 2.44(2.09~2.83) |
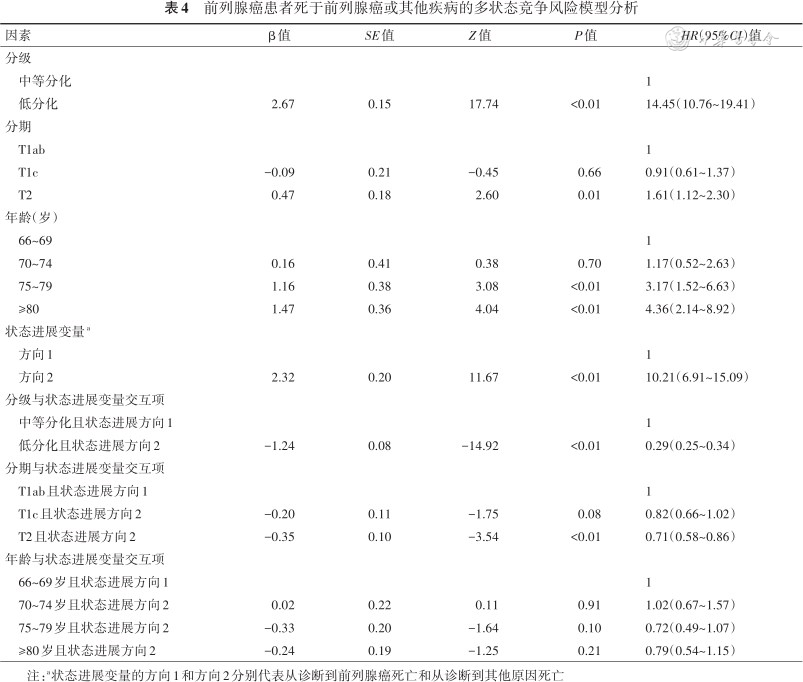
2. 多状态竞争风险模型的多因素分析:与中等分化相比,低分化的前列腺癌患者总体死亡风险显著增加[HR:14.45(95%CI:10.76~19.41)];与T1ab期相比,T1c期总体死亡风险差异没有统计学意义[HR:0.91(95%CI:0.61~1.37)],T2期总体死亡风险显著增加[HR:1.61(95%CI:1.12~2.30)]。同时,与状态转变方向1相比(从诊断到前列腺癌死亡),状态转变方向2(从诊断到其他原因死亡)的死亡风险显著增加[HR:10.21(95%CI:6.91~15.09)]。此外,与中等分化相比,低分化前列腺癌患者死于其他原因的风险低于死于前列腺癌本身的风险[HR:0.29(95%CI:0.25~0.34)];与T1ab期相比,T1c期前列腺癌患者死于其他原因的风险与死于前列腺癌本身的风险差异没有统计学意义[HR:0.82(95%CI:0.66~1.02)],T2期前列腺癌患者死于其他原因的风险低于死于前列腺癌本身的风险[HR:0.71(95%CI:0.58~0.86)];不同年龄组的前列腺癌患者死于其他原因的风险与死于前列腺癌本身的风险差异没有统计学意义。见表4。
前列腺癌患者死于前列腺癌或其他疾病的多状态竞争风险模型分析
前列腺癌患者死于前列腺癌或其他疾病的多状态竞争风险模型分析
| 因素 | β值 | SE值 | Z值 | P值 | HR(95%CI)值 |
|---|---|---|---|---|---|
| 分级 | |||||
中等分化 | 1 | ||||
低分化 | 2.67 | 0.15 | 17.74 | <0.01 | 14.45(10.76~19.41) |
| 分期 | |||||
T1ab | 1 | ||||
T1c | -0.09 | 0.21 | -0.45 | 0.66 | 0.91(0.61~1.37) |
T2 | 0.47 | 0.18 | 2.60 | 0.01 | 1.61(1.12~2.30) |
| 年龄(岁) | |||||
66~69 | 1 | ||||
70~74 | 0.16 | 0.41 | 0.38 | 0.70 | 1.17(0.52~2.63) |
75~79 | 1.16 | 0.38 | 3.08 | <0.01 | 3.17(1.52~6.63) |
≥80 | 1.47 | 0.36 | 4.04 | <0.01 | 4.36(2.14~8.92) |
| 状态进展变量a | |||||
方向1 | 1 | ||||
方向2 | 2.32 | 0.20 | 11.67 | <0.01 | 10.21(6.91~15.09) |
| 分级与状态进展变量交互项 | |||||
中等分化且状态进展方向1 | 1 | ||||
低分化且状态进展方向2 | -1.24 | 0.08 | -14.92 | <0.01 | 0.29(0.25~0.34) |
| 分期与状态进展变量交互项 | |||||
T1ab且状态进展方向1 | 1 | ||||
T1c且状态进展方向2 | -0.20 | 0.11 | -1.75 | 0.08 | 0.82(0.66~1.02) |
T2且状态进展方向2 | -0.35 | 0.10 | -3.54 | <0.01 | 0.71(0.58~0.86) |
| 年龄与状态进展变量交互项 | |||||
66~69岁且状态进展方向1 | 1 | ||||
70~74岁且状态进展方向2 | 0.02 | 0.22 | 0.11 | 0.91 | 1.02(0.67~1.57) |
75~79岁且状态进展方向2 | -0.33 | 0.20 | -1.64 | 0.10 | 0.72(0.49~1.07) |
≥80岁且状态进展方向2 | -0.24 | 0.19 | -1.25 | 0.21 | 0.79(0.54~1.15) |
注:a状态进展变量的方向1和方向2分别代表从诊断到前列腺癌死亡和从诊断到其他原因死亡
本研究通过案例分析系统地比较了传统比例风险模型、传统竞争风险模型和多状态竞争风险模型的优缺点。根据传统比例风险模型和传统竞争风险模型中分期变量与前列腺癌死亡的关联差异,和肿瘤分化程度与其他原因死亡的关联差异可以看到,相比传统比例风险模型,传统竞争风险模型在估计原因别死亡影响因素时更加严格或保守。因为前者没有将竞争结局事件记为删失,而是将已发生竞争结局事件的患者筛选出来用于计算竞争结局事件的累积发生风险,从而调整竞争结局事件对主要结局事件发生风险的影响。
通过传统竞争风险模型的分析结果,可以初步判断癌症分化程度与前列腺癌死亡[HR(95%CI):3.91(3.37~4.53)]与其他原因死亡的关联强度[HR(95%CI):1.03(0.95~1.12)]存在差异,但无法明确差异的大小。同样的问题也见于肿瘤分期与前列腺癌死亡和其他原因死亡的关联差异。即使是与前列腺癌死亡和其他原因死亡密切相关的年龄,根据传统竞争风险模型的分析结果,只能初步判断:相比66~69岁患者,75~79岁前列腺癌患者死于前列腺癌的风险[HR(95%CI):2.15(1.51~3.05)]可能高于死于其他疾病的风险[HR(95%CI):1.57(1.34~1.84)],但无法明确两者的具体差异。而在多状态竞争风险模型中,通过引入分级与状态进展变量的交互项,可以明确:与中等分化相比,低分化前列腺癌患者死于其他原因的风险是死于前列腺癌本身的0.29倍(P<0.05);不同年龄组的前列腺癌患者,死于其他原因的风险与死于前列腺癌本身的风险差异没有统计学意义(P>0.05)。
此外,从多状态竞争风险模型可以更加直接得出以下结论:(1)前列腺癌患者死于其他原因的风险显著高于死于前列腺癌本身的风险;(2)前列腺癌患者癌症相关特征(如分化程度和肿瘤分期)与前列腺癌死亡的关联显著高于与其他原因死亡的关联强度;(3)前列腺癌患者死于其他原因的主要影响因素是除已知的癌症相关特征和年龄之外的其他未知因素(即状态进展变量的潜在意义)。其中第一条结论最为关键,这与当前备受关注的癌种患者的心血管死亡风险显著升高,甚至可能高于肿瘤本身的死亡风险等观察性研究结果非常一致[13, 14, 15]。而这些结论从传统比例风险模型和传统竞争风险模型均无法得出。
从上述分析可以看出多状态竞争风险模型相比传统比例风险模型和传统竞争风险模型存在明显的优势:能构建更加符合真实世界关联模式的生存数据分析模型。然而多状态竞争风险模型最主要的两个局限在于:多状态结局变量分布类型的检验和不同结局状态合理进展方向的构建。如前所述,当多种结局状态仅由相互独立的吸收状态组成时,结局变量的分布类型检验相对容易;而当多种结局状态之间存在相互进展时,结局变量的分布类型尚无法直接检验。针对不同结局状态合理进展方向的构建,由于本篇文章采用的实例相对简单,比较容易明确不同结局状态之间合理的进展方向。而当结局状态相对较多时,如宫颈癌筛查的人群,可能在随访期间出现HPV感染,宫颈上皮内瘤样病变(cervical intraepithelial neoplasia,CIN)1级、2级和3级,早期宫颈癌、晚期宫颈癌,宫颈癌复发、转移,宫颈癌死亡、其他原因死亡等多种结局状态,尤其是当不同结局状态可以相互转化时,如CIN1、CIN2、CIN3均属于可逆性病变,及时治疗后均可逆转到健康宫颈上皮状态。在上述诸多结局状态之间构建出所有合理的进展方向,将是非常复杂的事情,也即需要构建相对完善的疾病自然史模型[16, 17, 18]。此外,稳健的多状态竞争风险模型不仅需要大样本的支持,更需要每种结局事件均有一定数量的样本支持。
综上,多状态竞争风险模型为多种结局事件的生存数据分析提供了很好的思路,也为完善疾病自然史研究提供了很好的思路。但多状态竞争风险模型同样存在诸多尚未解决的问题,未来需要更多的方法学研究来进一步多状态竞争风险模型,同时也需要更多样本量更大、设计更为严格的真实世界研究来验证多状态竞争风险模型的合理性。
install.packages("asaur")
install.packages("mstate")
install.packages("cmprsk")
library(asaur)
library(survival)
library(cmprsk)
library(mstate)
help(prostateSurvival)
data (prostateSurvival)
table(prostateSurvival$status)
status.alldeath<-{prostateSurvival$status != 0}
status.prost<-{prostateSurvival$status == 1}
status.other<-{prostateSurvival$status == 2}
prostateSurvival.Mat<-model.matrix(object =~grade+stage+ageGroup, data = prostateSurvival)
prostateSurvival.Mat<-prostateSurvival.Mat[, -1]
head(prostateSurvival.Mat)
#传统比例风险模型前列腺癌死亡影响因素分析
cph.PROSTATA.Mort<-coxph(Surv(survTime, event=status.prost)~prostateSurvival.Mat,
data=prostateSurvival)
summary(cph.PROSTATA.Mort)
#传统比例风险模型其他死亡影响因素分析
cph.OTHER.Mort<-coxph(Surv(survTime, event=status.other)~prostateSurvival.Mat,
data=prostateSurvival)
summary(cph.OTHER.Mort)
#传统竞争风险模型前列腺癌死亡影响因素分析
crr.PROSTATA.Mort<-crr(ftime = prostateSurvival$survTime, fstatus = prostateSurvival$status,
cov1 = prostateSurvival.Mat, failcode = 1, cencode = 0)
summary(crr.PROSTATA.Mort)
#传统竞争风险模型其他原因死亡影响因素分析
crr.OTHER.Mort<-crr(ftime = prostateSurvival$survTime, fstatus = prostateSurvival$status,
cov1 = prostateSurvival.Mat, failcode = 2, cencode = 0)
summary(crr.OTHER.Mort)
#多状态竞争风险模型分析
tmat<-trans.comprisk(2, names = c("event-free", "prostate", "other"))
attach(prostateSurvival)
prostate.long<-msprep(time = cbind(NA, survTime, survTime), status = cbind(NA, status.prost, status.other),
keep = data.frame(grade, stage, ageGroup), trans = tmat)
cuminc.prostate.MV<-coxph(Surv(time, status)~(grade)*trans+(stage)*trans+(ageGroup)*trans+
trans, data=prostate.long)
summary(cuminc.prostate.MV)



























