• 点赞 0
  • 分享 0
• 讲座 •
层次结构数据的分析方法及SPSS实现
中华老年医学杂志, 2020,39(10) : 1236-1240. DOI: 10.3760/cma.j.issn.0254-9026.2020.10.030
摘要

医疗卫生领域研究中常见的层次结构数据适用的3种统计模型包括混合线性模型(MLM)、广义估计方程(GEE)和广义线性混合模型(GLMM)。在IBM SPSS Statistics中，"混合模型"分析菜单下的"线性"和"广义线性"选项可分别实现MLM和GLMM，"广义线性模型"菜单下的"广义估计方程"可实现GEE。以IBM SPSS Statistics自带数据为例，展示在IBM SPSS Statistics 20.0中的实现并对主要结果进行解释，IBM SPSS Statistics可以简单地实现MLM、GEE和GLMM，3种方法考虑数据的聚集性并将误差分解到相应的层次水平，可以得到更为科学合理的结果，有利于广大医学研究者快速掌握并使用。

引用本文: 程锦, 程文炜, 刘晓芳, 等.  层次结构数据的分析方法及SPSS实现 [J] . 中华老年医学杂志, 2020, 39(10) : 1236-1240. DOI: 10.3760/cma.j.issn.0254-9026.2020.10.030.
参考文献导出:   Endnote    NoteExpress    RefWorks    NoteFirst    医学文献王
扫  描  看  全  文

正文
作者信息
基金 0  关键词  0
English Abstract
评论
阅读 0  评论  0
相关资源
引用 | 论文 | 视频

版权归中华医学会所有。

未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。

除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。

老年人群常由多种因素造成多病共存，且老年医学关注的疾病现象往往要从宏观和微观层面去解释，因而层次结构数据(hierarchically structured data)在老年医学研究中较为常见。层次结构数据是指数据具有多个层级或多个水平，如卫生服务或流行病学调查，研究对象常常嵌套于地区、城乡、医院等不同级别中；纵向研究中，可把时间视为水平1单位，每个研究对象视为水平2单位；多中心临床试验或动物实验中，常将患者或动物视为水平1单位，试验中心或动物窝别视为水平2单位。层次结构数据中同一层级的个体间往往不具备独立性，若采用传统分析方法可能忽略高水平单位间变异，残差标准误被高估，且忽略了高水平单位对结局变量的影响[1]。本文旨在介绍老年医学研究中层次结构数据适用的3种统计模型，这些模型通过拟合与数据层次结构相适应的复杂误差结构，并估计相应的残差方差及协方差，提高了模型估计的准确度[1,2,3]。本文采用IBM SPSS Statistics自带数据展示其在IBM SPSS Statistics 20.0中的实现过程和结果呈现，以期为医学科研人员正确运用此法提供便捷可行的途径。

一、层次结构数据统计模型简介
1．混合线性模型(mixed linear model，MLM)：

将单一的随机误差项分解到与数据层次结构对应的各水平上，估计相应的残差方差及协方差。借此，模型既可解释个体变异，也可估计高水平随机效应，提供高水平单位潜在的总体特征信息[4,5,6]。

2．广义估计方程(general estimation equation，GEE)：

在模型中引入作业相关矩阵，计算各次测量值两两之间的相关性，得到稳健的参数估计值，亦适用于处理观察次数不等、观察时间间隔不等的非平衡设计数据[7]。

3．广义线性混合模型(general linear mixed model，GLMM)：

基于混合线性模型发展而来，若因变量是离散型的，如是否患病、疾病的严重程度等，则混合线性模型即不再适用，通过连接函数衍生出适合处理此类层次结构数据的广义线性混合模型[2]。

3种模型适用情况见表1。

点击查看表格
表1

3种模型适用情况

表1

3种模型适用情况

统计模型因变量类型自变量与因变量的关系是否允许缺失值是否适用于非平衡设计数据是否可为3个或更多水平
混合线性模型定量线性是是是
广义估计方程定量/定性/等级线性/非线性是是否
广义混合线性模型定量/定性/等级线/非线性是是是
二、实例及软件实现
1．混合线性模型：

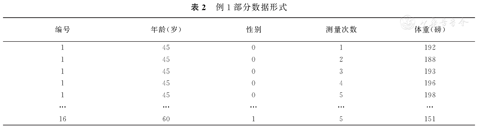
例1：16例患者接受为期6个月的新饮食，测量其对有心脏疾病家族史患者体重的影响，干预前和干预后共测量5次体重[8]，该数据来自SPSS安装目录下的Samples\English文件夹内的dietstudy.sav，为拟合混合线性模型，更改其数据格式见表2，其中测量次数为1、2、3、4、5分别代表第5次、第4次、第3次、第2次以及第1次测量，SPSS实现步骤如表3。其中，第②步选的是非结构化，表示对观测值之间的相关性不做任何限定，让模型根据资料特征自动估计。

点击查看表格
表2

例1部分数据形式

表2

例1部分数据形式

编号年龄(岁)性别测量次数体重(磅)
14501192
14502188
14503193
14504196
14505198
……………
166015151
点击查看表格
表3

混合线性模型SPSS实现

表3

混合线性模型SPSS实现

分析步骤说明
①"分析(analyze)"→"混合模型(mixed models)"→"线性(linear)"选择SPSS软件中的"混合线性模块"
②"指定主体和重复(specify subjects and repeated)"：编号放入"主体(subjects)"框，测量次数放入"重复(repeated)"框，"重复协方差类型(repeated covariance type)"选择"非结构化(unstructured)"指定数据层次结构和重复测量协方差类型
③"因变量(dependent variable)"：体重，"因子(factor)"：测量次数指定结局变量和自变量
④"固定效应(fixed effects)"：选择测量次数添加入"模型(model)"框中→"继续(continue)"指定固定效应
⑤"随机(random)"：直接点击"继续(continue)"指定随机效应
⑥"统计(statistics)"：选择"固定效应的参数估算值(parameter estimates)""协方差参数检验(tests for covariance parameters)"→"确定(ok)"指定参数估计及检验

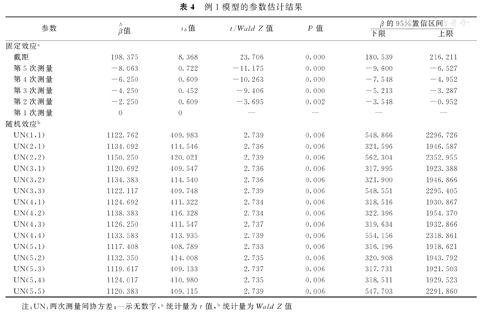
表4为参数估计结果，可以看出相对于第1次测量，每次测量的体重变化均有统计学意义。且任意2次测量间都是有相关性的，即数据具有层次结构。

点击查看表格
表4

例1模型的参数估计结果

表4

例1模型的参数估计结果

参数值sb值t/Wald Z值P值β的95%置信区间
下限上限
固定效应a      
 截距198.3758.36823.7060.000180.539216.211
 第5次测量-8.0630.722-11.1750.000-9.600-6.527
 第4次测量-6.2500.609-10.2630.000-7.548-4.952
 第3次测量-4.2500.452-9.4060.000-5.213-3.287
 第2次测量-2.2500.609-3.6950.002-3.548-0.952
 第1次测量00————
随机效应b      
 UN(1，1)1122.762409.9832.7390.006548.8662296.726
 UN(2，1)1134.092414.5462.7360.006321.5961946.587
 UN(2，2)1150.250420.0212.7390.006562.3042352.955
 UN(3，1)1120.692409.5472.7360.006317.9951923.388
 UN(3，2)1134.383414.5402.7360.006321.9001946.866
 UN(3，3)1122.117409.7482.7390.006548.5512295.405
 UN(4，1)1124.692411.3222.7340.006318.5161930.867
 UN(4，2)1138.383416.3282.7340.006322.3961954.370
 UN(4，3)1126.250411.5472.7370.006319.6341932.866
 UN(4，4)1133.583413.9352.7390.006554.1562318.861
 UN(5，1)1117.408408.7892.7330.006316.1961918.621
 UN(5，2)1132.350414.0082.7350.006320.9081943.792
 UN(5，3)1119.617409.1332.7370.006317.7311921.503
 UN(5，4)1124.017410.9802.7350.006318.5111929.523
 UN(5，5)1120.383409.1152.7390.006547.7032291.860

注：UN：两次测量间协方差；—示无数字，a统计量为t值，b统计量为Wald Z值

2．广义估计方程：

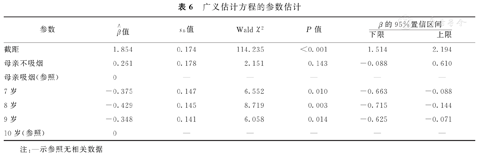
例2：一项空气污染对儿童健康影响的纵向研究，旨在分析儿童年龄和母亲吸烟情况对儿童喘鸣的影响[9]，收集俄亥俄州儿童在7、8、9和10岁的喘鸣症状及母亲在研究第1年吸烟情况。该数据来自SPSS安装目录下的Samples\English文件夹内的wheeze_steubenville.sav，包含如下变量：(1)id：儿童编号；(2)age：测量时儿童的年龄；(3)wheeze：测量时儿童喘鸣状况，0为无，1为有；(4)smoker：母亲在研究第1年的吸烟情况，0为不吸烟，1为吸烟；SPSS实现步骤见表5。表6给出了参数估计结果，无足够理由表明母亲吸烟影响儿童喘鸣发生(P＝0.143)，低年龄组(7～9岁组)相对于10岁组而言，喘鸣发生概率更高。作业相关矩阵是对观测值之间相关性的设定，可通过准似然独立准则(Quasi likelihood under independence model criteria，QIC)优选合适的作业相关矩阵，QIC值越小模型越合适[7]，此外，在SPSS中广义估计方程无法对残差进行深入分解[10]。

点击查看表格
表5

重复测量数据的广义估计方程的SPSS实现

表5

重复测量数据的广义估计方程的SPSS实现

分析步骤说明
①"分析(analyze)"→ "广义线性模型(generalized linear models)"→ "广义估算方程(generalized estimating equations)"选择SPSS软件中的广义估计方程模块
②"重复(repeated)"：将编号选入"主体变量(subjects variables)"框，年龄选入"主体内变量(within-subject variables)"框，"工作相关性矩阵(working correlation matrix)"选择"非结构化(unstructured)"指定数据层次结构和重复度量变量及重复测量间的相关性
③"模型类型(type of model)"：选择"二元Logistic(binary logistic)"选择连接函数为二分类Logistic
④"响应(response)"：将喘鸣状况选入"因变量(dependent variable)"框指定结局变量
⑤"预测变量(predictors)"：将母亲吸烟情况和年龄选入"因子(factors)"框指定自变量
⑥"模型(model)"：将母亲吸烟情况和年龄选入"模型(model)"框指定主效应(此部分也可以根据研究需要拟合交互效应)
⑦"估算(estimation)"：默认即可对模型的估计方法进行设定
⑧"统计(statistics)"：选择"工作相关性矩阵(working correlation matrix)"，其余默认即可指定估计的参数结果和工作相关矩阵
点击查看表格
表6

广义估计方程的参数估计

表6

广义估计方程的参数估计

参数值sb值Waldχ2P值β的95%置信区间
下限上限
截距1.8540.174114.235<0.0011.5142.194
母亲不吸烟0.2610.1782.1510.143-0.0880.610
母亲吸烟(参照)0—————
7岁-0.3750.1476.5520.010-0.663-0.088
8岁-0.4290.1458.7190.003-0.715-0.144
9岁-0.3480.1416.0580.014-0.625-0.071
10岁(参照)0—————

注：—示参照无相关数据

3．广义线性混合模型：

例3：某地为了解某新教学方法能否有效提升学生成绩，采用简单随机抽样选取23所学校，并随机抽取不同班级分为试验组和对照组，在新学年分别应用新教学法和常规教学法进行教学，学生在学年初和学年末各考试1次[11]；此数据有3个层次：学校、班级和学生(本数据为IBM SPSS Statistics自带数据，名为test_scores.sav，文件位置同例1)。SPSS实现步骤见表7。广义线性混合模型的输出结果需要双击阅读详细内容。

点击查看表格
表7

例3模型的SPSS实现

表7

例3模型的SPSS实现

分析步骤说明
①"分析(analyze)"→ "混合模型(mixed models)"→"广义线性(generalized linear)"选择SPSS软件中的"广义线性混合模块"
②将学校，班级，学生编号逐次拖入"主体(subjects)"区域["数据结构(data structure)"选项]指定数据层次结构
③"目标(target)"：选择年末考试成绩，连接函数选择"线性模型(linear model)"["字段和效应(fields & effects)"选项]指定结局变量和连接函数
④"固定效应(fixed effects)"：将学校位置、学校类型、教学方法、班级学生人数、性别、是否减免午餐以及年初成绩拖入"主(main)"区域["字段和效应(fields & effects)"选项]指定固定效应
⑤"随机效应(random effects)"：默认拟合学校和班级两个层次水平的随机效应指定随机效应
⑥"构建选项(build option)"：默认即可→"运行(run)"指定结局变量参考类别，最大迭代次数，置信区间等

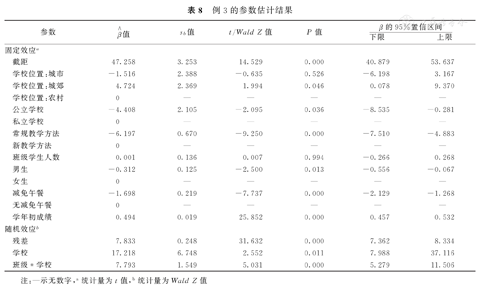
本模型输出结果包括：(1)模型摘要，包括设定的连接函数、残差概率分布和拟合信息标准等；(2)数据结构；(3)模型预测值和实际值的比较；(4)固定效应的估计值，默认以图形的方式给出结果，如需具体结果，可将"样式"框下拉切换为"表"；(5)固定效应的系数估计和检验结果；(6)协方差矩阵；(7)协方差参数和随机效应估计值的结果；(8)拟合模型的设定摘要。固定效应和随机效应参数估计结果及解释同案例1和2，故此处不赘述。表8为整合后的结果，残差被分解到学校和班级水平后，仍有统计学意义，学校水平组内相关系数(intra-class correlation coefficent，ICC)即组间方差与总方差之比[12]，ICC＝×100%=52.4%，班级水平的组内相关系数ICC＝×100%-23.7%，分别表示学校水平和班级水平组内成绩的相似程度，表明学生年末成绩在学校和班级水平有聚集性，即数据有层次结构，采用混合模型更为合适，结果表明新教学方法较常规教学方法更好地提高成绩(P<0.001)。

点击查看表格
表8

例3的参数估计结果

表8

例3的参数估计结果

参数值sb值t/Wald Z值P值β的95%置信区间
下限上限
固定效应a      
 截距47.2583.25314.5290.00040.87953.637
 学校位置：城市-1.5162.388-0.6350.526-6.1983.167
 学校位置：城郊4.7242.3691.9940.0460.0789.370
 学校位置：农村0—————
 公立学校-4.4082.105-2.0950.036-8.535-0.281
 私立学校0—————
 常规教学方法-6.1970.670-9.2500.000-7.510-4.883
 新教学方法0—————
 班级学生人数0.0010.1360.0070.994-0.2660.268
 男生-0.3120.125-2.5000.013-0.556-0.067
 女生0—————
 减免午餐-1.6980.219-7.7370.000-2.129-1.268
 无减免午餐0—————
 学年初成绩0.4940.01925.8520.0000.4570.532
随机效应b      
 残差7.8330.24831.6320.0007.3628.334
 学校17.2186.7482.5520.0117.98837.116
 班级*学校7.7931.5495.0310.0005.27911.506

注：—示无数字，a统计量为t值，b统计量为Wald Z值

三、讨论与小结

通常，MLM中"混合"主要是指模型中既包含固定效应也包含随机效应[13]，而GEE和GLMM中"广义"是指该类模型通过联接函数将因变量和线性预测值关联起来克服了线性模型要求因变量服从正态分布的限制[14]。从模型选择来看，MLM和GLMM可以通过随机效应的设置，描述和分析个体变化趋势的特征，而GEE是从人群的视角进行分析。从软件选择来看，与SAS、R、Stata、Mplus，以及专门用于多水平分析的MlwinN等软件比较，IBM SPSS Statistics具有简便易操作、更易掌握的优势[1]。

利益冲突
利益冲突

所有作者均声明不存在利益冲突

参考文献
[1]
钱莎莎，邢健男，王璐．多水平统计模型分析方法及其应用[J]．中国公共卫生，2017，33(9): 1414-1416.DOI: 10.11847/zgggws2017-33-09-30.
QianSS, XingJN, WangL．Multilevel statistical model analysis and its application[J]．Chin J Public Health，2017，33(9): 1414-1416.DOI: 10.11847/zgggws2017-33-09-30.
[2]
孙振球，徐勇勇．医学统计学(第4版)[M]．北京：人民卫生出版社，2014：352-368.
SunZQ, XuYY.Medical statistics(4th edition)[M]．Beijing：People's Medical Publishing House，2014：352-368.
[3]
ChungH, BeretvasSN.The impact of ignoring multiple membership data structures in multilevel models[J]．Br J Math Stat Psychol，2012，65(2): 185-200.DOI: 10.1111/j.2044-8317.2011.02023.x.
[4]
兰彤彤．基于线性混合模型的尼古丁依赖的遗传度研究[D]．太原：山西医科大学，2019.
LanTT.Heritability of nicotine dependence based on linear mixed model[D]．Taiyuan：Shanxi Medical University，2019.
[5]
严涛．基于变参数和混合模型的医学纵向数据研究[D]．南昌：南昌大学，2014.
YanT．Medical longitudinal data research based on variable parameter models and mixed models[D]．Nanchang：Nanchang University，2014.
[6]
彭慧．多水平模型在中学生预防艾滋病健康教育中的应用[D]．广州：中山大学，2009.
PengH．The application of multilevel model for health education on AIDS prevention among secondary school students[D]．Guangzhou：Sun Yat-sen University，2009.
[7]
朱玉，王静，何倩．广义估计方程在SPSS统计软件中的实现[J]．中国卫生统计，2011，28(2): 199-201.DOI: 10.3969/j.issn.1002-3674.2011.02.031.
ZhuY, WangJ, HeQ．The implementation of generalized estimation equation in SPSS[J]．Chin J Health Statistics，2011，28(2): 199-201.DOI: 10.3969/j.issn.1002-3674.2011.02.031.
[8]
IBM Knowledge Center.Using linear mixed models to analyze repeated measurements[EB/OL]．[2020-01-05]．https://www.ibm.com/support/knowledgecenter/zh/SSLVMB_25.0.0/statistics_casestudies_project_ddita/spss/tutorials/mixed_diet_intro.html.
[9]
IBM Knowledge Center.Using generalized estimating equations to fit a repeated measures logistic regression[EB/OL]．[2020-01-05]．https://www.ibm.com/support/knowledgecenter/SSLVMB_24.0.0/spss/tutorials/gee_wheeze_intro.html.
[10]
杨珉，李晓松．医学和公共卫生研究常用多水平统计模型[M]．北京：北京大学医学出版社，2007.
YangM, LiXS.Multilevel statistical models commonly used in medical and public health research[M]．Beijing：Peking University Medical Press，2007.
[11]
IBM Knowledge Center.Analyzing test scores(generalized linear mixed models)[EB/OL]．[2020-01-05]．https://www.ibm.com/support/knowledgecenter/zh/SSLVMB_25.0.0/statistics_casestudies_project_ddita/components/glmm/glmm_testscores_intro.html.
[12]
郝光．睡眠和心血管疾病的关联研究[D]．北京：北京协和医学院，2015.DOI：10.7666/d.Y2817867.
HaoG．Correlations between sleep pattern and cardiovascular diseases in a Chinese middle-aged population[D]．Beijing：Peking Union Medical College，2015.DOI：10.7666/d.Y2817867.
[13]
黄坤，倪宗瓒，程薇波．混合线性模型在临床试验中重复测量资料的应用[J]．现代预防医学，2005，32(11): 1584-1585.DOI: 10.3969/j.issn.1003-8507.2005.11.014.
HuangK, NiZZ, ChengWB.Mixed linear model for the repeated measure data in clinical trials[J]．Modern Preventive Medicine，2005，32(11): 1584-1585.DOI: 10.3969/j.issn.1003-8507.2005.11.014.
[14]
路凤，李亚伟，李成橙，等．时间序列分析在空气污染与健康领域的应用及其R软件实现[J]．中国卫生统计，2018，35(4): 622-625.
LuF, LiYW, LiCC，et al.Application of time series analysis in the field of air pollution and health and its R software implementation[J]．Chin J Health Statistics，2018，35(4): 622-625.
　
　
展开/关闭提纲
查看图表详情
回到顶部
放大字体
缩小字体
标签
关键词
统计学模型
线性模型
喘鸣
广义估计方程
广义线性模型
统计模型
混合模型
层次结构
参数估计
分析方法