版权归中华医学会所有。
未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
中断时间序列（interrupted time-series，ITS）设计是收集干预前后多个时间点的结果数据，在控制了结果变量干预前的下降或上升趋势后，用统计学模型评价干预措施的效果，包括干预点前后的水平变化和趋势变化。从研究设计的角度，ITS属准实验设计，在缺少有效对照的情况下，ITS设计能够得到稳健的估计结果。Box和Tiao[1]最早提出了ITS分析方法，由于ITS多应用常规收集的数据，使用干预前后对比，并不需要一个平行的对照，ITS在国外社会政策、药物政策和环境政策有广泛的应用[2]，但在卫生政策、卫生项目和措施评价中应用并不多，在国内ITS还鲜为广大的卫生工作者熟知。
ITS分为单组ITS设计和带有比较组的ITS设计，因ITS设计主要用于常规收集时间间隔相等点的干预前后指标的比较，所以单组ITS设计更为常用，其设计原理见图1。横坐标为时间点，测量间隔相等，以○代表，如日、月、年等，X表示干预的时间点；纵坐标为测量某项指标的数或率，如脑卒中死亡数（率）、交通事故发生数（率）、交通伤害发生数或死亡数（率）、疫苗接种数（率）、住院或门诊就诊数（率）和分娩数（率）等。
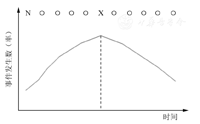
在统计分析时，ITS分析对干预实施前和实施后两个时间段进行线性回归分析，分析干预因素作用的水平改变和斜率改变，应用间断线性回归模型（segmented linear regression model）[3]，见图2。此分析可检验试验前后在干预点水平下降或升高的幅度是否有统计学意义，及在干预实施后某事件率或数随时间下降或上升的斜率是否与试验前不同，其主要优势是控制了试验前某事件率或数已随时间下降或上升的趋势。当时间序列数据在干预前和干预后呈现线性趋势时，可应用线性回归模型来拟合数据，探讨干预措施对结果变量的影响。
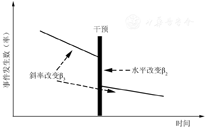
ITS分析拟合分段的多重线性回归[4]。令X1是计数的时间变量, X1＝1, 2, 3，…, n；X2指示干预，干预前的观察X2＝0，干预后的观察X2＝1；X3表示斜率，设X3＝0指示干预前的观察, X3＝X1指示干预后的观察。拟合水平和斜率改变模型如下：
Yt＝β0＋β1X1＋β2X2＋β3X3＋∑βjXj＋εt
∑βjXj表示一组协变量，这里暂不考虑协变量。将变量X1、X2和X3代入上式，试验前：X1＝1, 2，…, n，X2＝X3＝0，则模型为：
Yt＝β0＋β1X1＋εt
干预后：X2＝1, X3＝X1，则模型为：
Yt＝β0＋β1X1＋β2X2＋β3X3＋εt＝β0＋β1X1＋β2×1＋β3X1＋εt＝（β0＋β2）＋（β1＋β3）X1＋εt＝β0*＋β1*X1＋εt
β0*和β1*称为调整参数。β1为干预前的斜率, β2是水平改变量, β3是斜率改变量，（β1＋β3）是干预后的斜率；回归系数的假设检验就是水平改变量和斜率改变量的显著性检验。
间断线性回归模型的应用条件除上面提到的结果变量在干预前后随时间呈线性趋势外，还要求序列不存在自相关。用Durbin-Watson（DW）法检验序列是否存在1阶自相关，DW值在0~4之间，其值接近2或4表明无自相关。如果序列存在自相关，两种方法处理：①使用广义最小二乘估计（generalized least square estimator），而非最小二乘估计，对于STATA，使用"paris"而非"reg"来执行线性回归；对于SAS，使用"proc autoreg"而非"proc reg"，同时选取校正方法（如Yule-Walker法）和指定滞后阶数（nlag）来控制自相关。②使用多水平统计模型（随机截距和随机系数）检验1阶自回归水平协方差结构[1]。
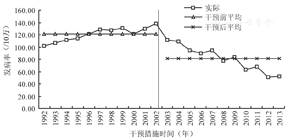
某市曾是乙型肝炎（乙肝）的高流行地区，从2002年开始，将乙肝疫苗纳入免疫规划，对新生儿、大学生、工人等重点人群实行扩大免疫规划策略，免费接种乙肝疫苗。1992-2013年发病率见表1，在2002年发病率达到了高峰（图3）。
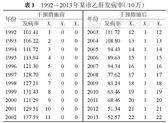
1992-2013年某市乙肝发病率（/10万）
1992-2013年某市乙肝发病率（/10万）
| 年份 | 干预措施前 | 年份 | 干预措施后 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 发病率 | X1 | X2 | X3 | 发病率 | X1 | X2 | X3 | ||
| 1992 | 101.41 | 1 | 0 | 0 | 2003 | 111.72 | 12 | 1 | 12 |
| 1993 | 106.22 | 2 | 0 | 0 | 2004 | 108.80 | 13 | 1 | 13 |
| 1994 | 111.72 | 3 | 0 | 0 | 2005 | 94.43 | 14 | 1 | 14 |
| 1995 | 113.94 | 4 | 0 | 0 | 2006 | 89.63 | 15 | 1 | 15 |
| 1996 | 121.30 | 5 | 0 | 0 | 2007 | 94.34 | 16 | 1 | 16 |
| 1997 | 128.70 | 6 | 0 | 0 | 2008 | 77.62 | 17 | 1 | 17 |
| 1998 | 127.21 | 7 | 0 | 0 | 2009 | 83.24 | 18 | 1 | 18 |
| 1999 | 131.43 | 8 | 0 | 0 | 2010 | 63.46 | 19 | 1 | 19 |
| 2000 | 121.29 | 9 | 0 | 0 | 2011 | 68.46 | 20 | 1 | 20 |
| 2001 | 129.51 | 10 | 0 | 0 | 2012 | 51.34 | 21 | 1 | 21 |
| 2002 | 137.59 | 11 | 0 | 0 | 2013 | 52.57 | 22 | 1 | 22 |
本例为单组ITS设计，2002年是实施扩大免疫规划策略开始，从图3可见乙肝发病率最高点出现在2002年。这个例子就是要回答扩大免疫规划策略是否影响时间序列的问题。即实施了某项干预措施或政策，时间序列被中断，为ITS设计。分析乙肝疫苗的扩大免疫规划策略对乙肝发病率的影响。
（1）干预措施前后的乙肝发病率：干预措施前（1992-2002年）该市乙肝的平均发病率120.938/10万，干预措施后（2003-2013年）该市乙肝平均发病率81.419/10万，干预措施后平均发病率比干预措施前减少了39.519/10万。
（2）水平改变模型：以1992-2002年为干预前，2003-2013年为干预后, X1、X2和X3的编码见表1。以发病率为因变量, X2为自变量，拟合简单线性回归模型：
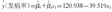
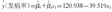
X2＝0时，干预前的乙肝发病率（/10万）：
X2＝1时，干预后的乙肝发病率（/10万）：
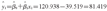
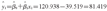
回归系数-39.519给出了干预措施对乙肝发病率水平改变的影响，因为回归系数为负数，实际上干预措施后的乙肝发病率比干预措施前减少了39.519/10万，回归系数
的t检验, P<0.000 1，差异有统计学意义，见图3。
（3）水平和斜率改变模型：按表1编码，拟合多重线性回归，得到水平和斜率改变模型为：
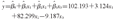
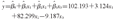
各自变量回归系数的t检验，
、
和
均<0.000 1，差异有统计学意义。干预前斜率是3.124，呈上升趋势；干预后，斜率是＋3.124-9.187＝-6.063，呈下降趋势；斜率改变量为
＝-9.187。干预前后乙肝发病率的改变量
＝82.299，为正值，干预后发病率减少，见图4。
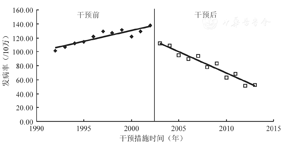
ITS研究收集的数据是干预措施前后多时间点的数据，能够定量的检测和评价干预措施是否有效，是时间序列数据中，评估干预措施效果最强的准实验设计，很难用随机对照试验评价干预措施的作用，ITS是非随机对照设置下强有力的统计分析方法，广泛应用于疾病监测数据分析，如果是单组ITS，不需设立对照组，可充分地利用监测资料得到可靠的估计结果[5,6,7]。ITS的优势在于干预措施实施后，评价干预效果从两个方面，一个是干预点前后下降幅度；进一步，ITS还可评价项目实施后的"长期趋势"的变化，即评价因变量的变化趋势。如某医院护士伤害发生干预效果评价，伤害发生率在干预前已呈下降的趋势，实施干预措施后，伤害发生率下降的斜率更陡，即斜率为负且与干预前相比，斜率差异有统计学意义，也说明干预措施有效，常用的统计方法如均值加环比和横断面观察研究等，达不到评价干预措施的目的，因没有控制干预前的趋势。ITS也形象的展示了干预措施是否是长期的或是暂时的作用及作用的强度，也能估计不同时间点的作用大小，估计时间作用趋势的变化[7]。
ITS要求干预前后因变量的变化趋势为线性，此时可用前述的分段回归分析。但时间序列数据可能存在季节性和周期性，此时可用自回归移动平均（auto-regressive integrated moving average，ARIMA）分析[8]。ARIMA模型常用于预测某指标，如手足口病和丙型肝炎的发病数（率），根据以前的时间序列数据建立的模型来预测未来。ARIMA模型通过捕捉序列数据中时间序列趋势来控制非平稳性（non-stationarity）或季节性（seasonality），以及控制序列的自相关。ARIMA模型在分析ITS数据上受到限制，因为① ARIMA模型拟合ITS数据比较复杂，要用到复杂的统计分析技术，尤其建立最好的简约模型比较困难。②通常使用100个时间序列点建立的ARIMA模型才稳定，但实际监测数据很难达到这一要求。③该方法是根据经济测量学发展起来的，多用于测量指标的预测而非解释测量指标。
ITS应用的样本含量，一般认为使用ITS模型干预前后应各有20个观察点，且呈线性或近似线性关系；如使用ARIMA拟合ITS模型，干预前后应各有50点，如果序列太短，尤其差分后，模型没有足够的把握度，并且统计检验很难检出有差异的干预效应。在实际模型拟合时多采用间断线性回归模型，在序列非平稳或存在季节效应时才考虑使用ARIMA模型。另外，间断线性回归分析时引入月份哑变量调节时间序列的季节性变化；也可将异常的月份，将1月和2月设为哑变量（1月和2月编码为1，否则为0），将哑变量放入模型进行调整。
应用ITS时应注意：①ITS是准实验设计，非常困难作因果关系的推断[9]。ITS分析可确定结果变量在干预后是否有水平和趋势改变，但不能确定这种改变与干预措施有明确的因果关系，因伴随的其他解释变量可直接或间接地影响结果变量。此外，ITS设计还可在单组（试验组）ITS的基础上，再增加一个平行对照组，试验组在干预前后比较的同时，还可与对照组比较，以控制同期非实验因素的干扰，得到干预措施与结果联系的更可靠结论。②ITS分析也依靠应用了多少个观察点，尤其当样本量（观察点）少时，更多地反映了结果变量"短期改变"而不是"长期趋势"。③常规监测数据虽然容易获得，且不需花费太多的数据收集经费，但存在数据质量的问题，如数据不完整、报告错误以及数据标准在不同的时间段可能不同。
