研究截至2020年1月31日新型冠状病毒肺炎疫情的早期流行动态，估计该疫情的基本再生数（R0）、潜伏期和世代间隔等流行病学参数。
使用威布尔、伽马和对数正态分布拟合从报告病例信息中获取的潜伏期和世代间隔数据的概率分布，采用Akaike信息准则确定最优模型。考虑到疫情还在流行中，应用指数增长模型拟合了2020年1月15-31日的疫情数据，并利用指数增长法、最大似然法和SEIR模型估计R0。
截至2020年1月26日早期疫情遵循指数增长模式，随后增长趋势有所减缓。平均潜伏期为5.01（95%CI：4.31~5.69）d；平均世代间隔为6.03（95%CI：5.20~6.91）d。3种方法估计的R0分别为3.74（95%CI：3.63~3.87），3.16（95%CI：2.90~3.43）和3.91（95%CI：3.71~4.11）。
世代间隔和潜伏期都更符合伽马分布，世代间隔均值比潜伏期均值长1.02 d；R0较高，疫情形势较为严峻；1月26日是疫情动态的一个转折点，之后疫情增长趋势有所减缓。
版权归中华医学会所有。
未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
2019年12月31日，湖北省武汉市暴发原因不明的肺炎，随后WHO确认这是由一种新型冠状病毒引起的。自2019年12月12日以来，武汉市卫生健康委员会报告了27例新型冠状病毒肺炎（COVID-19）病例，其中7例为重症病例。截至2020年1月31日24：00，中国内地共报告COVID-19确诊病例11 791例[1]。COVID-19传播途径主要是经呼吸道飞沫传播，目前大多数病例与密切接触有关，并且人群普遍易感。
由于"春运"的到来，大规模的人口移动，使得全国大部分区域受到COVID-19不同程度的威胁，部分区域出现输入和暴发疫情。传染病的传播潜力通常以基本再生数（R0）、暴发高峰时间、高峰值及持续时间等流行病学特征描述，COVID-19疫情的这些特征目前尚未达成普遍共识。2020年1月13日，武汉市宣布进入公共卫生应急状态，23日，中国政府对湖北省（除神农架）城市人口流动进行了限制。在当前和不断发展的干预措施下，持续地、及时地分析疫情发展趋势和流行病学特征及其动态具有重要意义，能为COVID-19疫情的科学防控提供依据。
疫情暴发后，已有学者开展了COVID-19流行病学参数估计的研究。Read等[2]通过拟合传播模型，估计COVID-19的R0在3.6~4.0之间，需要通过防控措施切断72%~75%的病毒传播才能阻止疫情的增长；Tang等[3]通过模型参数化估算出COVID-19的R0为6.47，并给出了疫情的达峰时间以及最终感染规模。Liu等[4]使用截至2020年1月23日的830例COVID-19确诊病例，估算出平均潜伏期为4.8 d，采用EG（Exponential Growth）和ML（Maximum Likelihood）法估计的R0分别为2.90（95%CI：2.32~3.63）和2.92（95%CI：2.28~3.67）；Wu等[5]使用基于SEIR的集合种群（metapopulation）模型模拟主要城市的流行病，并用马尔科夫链蒙特卡洛方法估计R0为2.68（95%CI：2.47~2.86）。
本研究的目的是分析COVID-19早期的流行病学特征，根据报告病例数据估计潜伏期和世代间隔的分布，并应用3种方法对R0进行估计，评估不同方法对其估值的影响。
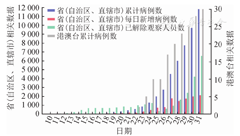
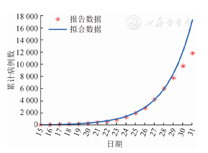
病例数据源于国家和各省份卫生健康委员会每日更新的日累计病例数及相关网站报告的病例和密切接触人群等信息，截至2020年1月31日，全国报告确诊病例为11 791例。收集的信息包括报告病例的累计数，每日新增病例数，已解除医学观察人员累计数（图1）。其中2020年1月1-15日每天报告的累计病例数均为41例，期间无新增病例。
潜伏期为一个感染者的被感染时间与其出现临床症状的时间之差[6]，世代间隔指一个感染者的被感染时间与其下一代感染者的被感染时间之差[7]。潜伏期的估计至关重要，是确定暴露人员隔离期限和判断病例感染时间的重要依据，同时也是流行病学预测模型的关键参数；世代间隔代表了疾病从一个人传至另一个人的平均间隔时间，世代间隔时间越短疫情越容易呈现暴发模式。部分病例接触传染源的时间不能直接观察到，这导致对潜伏期的估计较为困难。通常我们不能精确地观察到暴露于传染源和症状出现的时间，它们可能落入某些间隔。但可通过确定每个病例暴露的最早和最晚时间以及出现症状时间之差估计潜伏期，将此时间视为每个人潜伏期的区间截断估计值[8]。
为了估计潜伏期的
和s，我们采用威布尔[6,8,9]、伽马[6,8,10]和对数正态[6,8,11]3种概率密度分布模型拟合相关数据。通过对数据的定性分析比较拟合效果，为了使分析更加准确，又采用Akaike信息准则（AIC）进行定量分析[10]，其中，AIC值越小说明模型越适合。上述分析应用R 3.6.2和MATLAB 2014b软件完成。通过对比报告数据与模型拟合值的概率密度图，结合AIC值可确定出最优分布，再利用Bootstrap方法进行1 000次重采样计算
的95%CI[12]。对世代间隔数据采用相同的方法进行分析和计算。
R0是流行病模型中的一个重要参数，表示在发病初期，当所有人均为易感者时，一名病例在其患病期内所传染的平均人数。当R0>1时，流行病会暴发；否则疫情将会结束。
对于新出现的传染病暴发疫情，在疾病暴发初期，多数情况下病例数会呈现指数增长的模式。世代间隔的分布决定了指数增长率和R0之间的函数关系[13,14]。本文采用的R0计算方法有以下3种：
（1）定义r为累计感染病例数的指数增长率，C（t）为COVID-19的累计病例数。在初始阶段，累计病例数往往呈指数增长，但这个指数增长阶段到底会持续多久就需要人们进行判定。本研究采用拟合优度系数R2的大小判断初始指数增长阶段的持续时间长度。由于病例数是整数值，因此采用泊松回归估计该参数[14]。参照文献[13]计算R0：
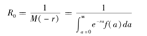
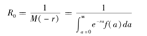
式中M（-r）是世代间隔分布f（a）的矩生成函数。
（2）假设二代病例服从期望值为R0的泊松分布，令N0，N1，…，NT表示连续单位时间内的病例数，世代间隔用ω表示，则R0可以由最大化对数似然估计函数估出[15]：
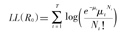
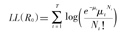
式中
，该方法要用在指数增长阶段。
（3）应用经典的传染病SEIR仓室模型分析中国COVID-19的传播动态。需要强调：SEIR数学模型中的暴露人群[E（t）]是指暴露但不具有传染性的人群。由于该疾病潜伏期后期可能具有传染性[16]，故模型中将具有传染性的潜伏期病例归为感染类I，暴露类E为无传染性的暴露人员，从而疫情传播动态可以使用以下微分方程组描述：
式中β表示传播系数，k是暴露类到感染类的转移率（数值上1/k即为感染后但无传染性时期的平均长度），γ表示移出率（数值上1/γ即为具有传染性时期的平均长度）。通过最小二乘法拟合累计病例数可以在适当的参数值范围内估计出模型中的3个参数值，进而通过下一代矩阵方法[17]给出的计算公式：
。
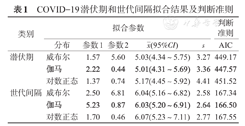
模型结果表明，3种分布的参数模型拟合值与非参数估计值基本一致（图2，图3），潜伏期的估计以伽马分布对应的AIC值最小，故潜伏期更倾向于伽马分布，潜伏期
为5.01（95%CI：4.31~5.69）d，s为3.36 d；拟合世代间隔时，仍然是伽马分布对应的AIC值最小，意味着世代间隔也更符合伽马分布，世代间隔
为6.03（95%CI：5.20~6.91）d，s为2.64 d（表1）。
COVID-19潜伏期和世代间隔拟合结果及判断准则
COVID-19潜伏期和世代间隔拟合结果及判断准则
| 类别 | 拟合参数 | 判断准则 | ||||
|---|---|---|---|---|---|---|
| 分布 | 参数1 | 参数2 |  (95%CI) | s | AIC | |
| 潜伏期 | 威布尔 | 1.57 | 5.60 | 5.03(4.34～5.75) | 3.27 | 449.17 |
| 伽马 | 2.22 | 0.44 | 5.01(4.31～5.69) | 3.36 | 447.57 | |
| 对数正态 | 1.37 | 0.74 | 5.17(4.45～5.92) | 4.41 | 451.52 | |
| 世代间隔 | 威布尔 | 2.50 | 6.81 | 6.04(5.16～6.82) | 2.58 | 167.34 |
| 伽马 | 5.23 | 0.87 | 6.03(5.20～6.91) | 2.64 | 166.50 | |
| 对数正态 | 1.70 | 0.46 | 6.07(5.23～7.11) | 2.77 | 167.55 | |
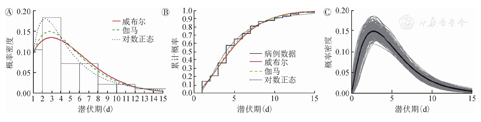
注：A：柱状图为90个病例潜伏期的频率分布；B：使用威布尔、伽马和对数正态分布模型估计的累计分布曲线与病例数据曲线进行比较；C：1 000次Bootstrap重采样数据拟合的潜伏期伽马分布（仅显示了300次样数据拟合值与平均值）
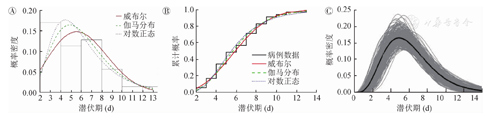
注：A：柱状图为35个病例世代间隔的频率分布；B：使用威布尔、伽马和对数正态分布模型估计的累计分布曲线与病例数据曲线进行比较；C：1 000次Bootstrap重采样数据拟合的世代间隔伽马分布（仅显示了300次样数据拟合值与平均值）
基于拟合优度系数R2（图4），累计病例数对应的指数增长期为12 d（对应于2020年1月26日），相应的指数增长率为0.383（95%CI：0.366~0.400）。指数增长曲线拟合结果见图5，拟合结果表明27日之后的增长率有所降低。由于在方法1和方法2两种计算R0的方法中均涉及到世代间隔，而从现有数据已经获得了世代间隔的估计值（表1），从而应用方法1和方法2可计算出R0值分别为3.74（95%CI：3.63~3.87）和3.16（95%CI：2.90~3.43）。对于SEIR模型法，当采用SEIR模型拟合截至1月27日的数据时拟合效果整体最优，如果再纳入27日之后更多的数据点进行拟合的话，整体拟合误差急剧增加。因此本研究采用最小二乘法基于截至27日的数据拟合得到了SEIR模型中的参数值为：传播率β=1.327，1/k=2.579，1/γ=2.950，进而计算出R0=3.91（95%CI：3.71~4.11）。拟合效果见图6。
已有研究显示，新型冠状病毒是一种类似于MERS和SARS的冠状病毒[18]，蝙蝠可能是该病毒的自然宿主[19]。早期，武汉人群中发生的不明原因肺炎被认为与武汉华南海鲜市场的暴露有关，后被证实致病原为新型冠状病毒[20]。随着疫情的发展，越来越多的病例被报道并未到过该海鲜市场，以及后期出现的家庭和医务人员聚集性病例的发生[21,22]，表明了该病存在"人-人"的传播途径。
根据截至2020年1月31日的新型冠状病毒每日累计病例数，本研究使用指数增长法、最大似然法和经典SEIR模型估算早期疫情的R0。在前两种方法中，再生数对于世代间隔的变化较为敏感，Yan[23]指出世代间隔=潜伏期+传染期，本研究根据对潜伏期与世代间隔的估计可知，两者的差值为1.02 d，这些估值可以为相应数学模型中的参数设置提供参考，也有助于我们继续深入分析传染期的分布情况。此外，我们希望能在今后的工作中搜集到更多传播链数据，以便更准确地估计出潜伏期、世代间隔等传染病相关参数的估值及分布。
3种方法计算出的R0值都明显>1，平均为3.60，高于SARS（R0=2.7）[24]和MERS（R0=2.0~2.8）[25]。这意味着COVID-19疫情还处于暴发期，形势较为严峻。
拟合优度系数R2表明，1月26日是疫情发展的一个转折点，同时指数增长曲线和SEIR模型拟合结果均显示1月27日之后实际疫情数据比拟合数据明显偏低，表明后续疫情增长趋势有所减缓。综合以上分析，我们认为1月26日是疫情动态的一个转折点，之后疫情增长趋势有所减缓，这应该是1月23日起政府采取的高效且强力的防控措施所带来的效果，防控措施对COVID-19疫情的影响还需通过对后继的更多数据进行分析才能得以验证和评估。
此外，WHO报告的人与人（直接）传播的R0在1.4~2.5之间，文献[4，26]中基于SARS或MERS的世代间隔对R0进行了估计，所得R0范围为2~3。本研究基于指数增长和最大似然及SEIR模型计算出的基本再生数数值高于他们的结果，一个潜在的因素是我们的数据是基于疫情早期指数增长阶段数据计算的，体现了疫情早期的传播特点。另外，R0的估算对世代间隔分布的变化较为敏感，现阶段受限于流行病学调查数据样本数据量偏少，该参数的估计可能存在偏倚，进而可能出现高估。
在模型的选取中，本研究选用经典的SEIR模型模拟此次疫情发展情况，模型对疫情早期的数据拟合效果良好，在后续研究中，我们将在模型中加入防控措施等因素，不断完善模型的构建，以及基于更多的疫情数据修正对参数的估值。这些工作还需基于医学专家们对COVID-19更深入的研究以及依赖更详细的流行病学调查数据。此外，隐性感染者不仅具有传染性，而且难以被发现，对其传播力的估算是当前研究的重要内容，对于疫情的防控决策至关重要，这也需我们在将来的研究工作中加以考虑。
所有作者均声明不存在利益冲突
