正畸牙移动是通过正畸力的刺激作用引起牙周膜、牙槽骨等牙周组织发生改建而实现的。牙周膜是连接牙骨质与牙槽骨之间的纤维结缔组织，具有支持牙齿传递、吸收和分散咬合力的作用。当正畸力施加于牙齿上时，载荷通过牙周膜从牙齿传递至牙槽骨，牙周膜的改建与牙槽骨的形成和吸收交替进行且互为作用。作为正畸牙移动的始动因素，牙周膜的应力/应变参与牙槽骨的改建过程，并影响牙齿的移动速度。因此，牙周膜的生物力学特性受到广泛关注。对正畸牙移动中牙周膜的结构变化和生物力学特性以及牙周膜的力学本构模型相关研究进行综述，讨论其力学响应和生物力学机制，以期为临床正畸牙移动精确数值模拟提供理论依据。
版权归中华医学会所有。
未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
正畸牙移动是通过力学刺激引起牙周膜、牙槽骨等牙周组织发生改建而实现的。经典的拉-压应力学说认为，作用于牙齿的正畸力最先引起牙周膜组织形态发生改变，形成拉力侧和压力侧；拉力侧牙周膜胶原纤维拉伸，促进成骨细胞增殖活化，在牙槽骨表面形成新骨；压力侧牙周膜则出现玻璃样变性并伴随明显的免疫炎症应答反应；待坏死的玻璃样变组织被完全清除，新的牙周膜组织形成后，在持续的压应力下牙槽骨开始在破骨细胞作用下发生直接性骨吸收，此时牙齿发生移动。牙周膜的重建是正畸牙移动的基础，与牙槽骨的增生和吸收交替进行且互为作用。牙周膜的应力/应变作为正畸牙移动的始动因素参与牙槽骨的重建过程，影响牙齿的移动方向和速度[1]，其生物力学特性值得深入研究。本文就正畸牙移动中牙周膜的结构及生物力学特性变化、牙周膜的生物力学响应及本构模型相关研究进行综述，并对未来研究进行展望，以期为正畸牙移动精确数值模拟提供理论依据。
牙周膜是连接牙骨质与牙槽骨之间的纤维结缔组织，使牙齿固位于牙槽窝内，具有传递、吸收和分散咬合力的作用。牙周膜结构复杂，由细胞、纤维和基质组成，富含血管、淋巴管和神经。牙周膜内的细胞包括成纤维细胞、牙周膜干细胞、成牙骨质细胞、成骨细胞及破骨细胞等，是正畸力加载后牙周生物学组织改建的来源。纤维主要包括胶原纤维（Ⅰ型、Ⅲ型和Ⅴ型胶原）和弹力纤维，其中胶原纤维数量最多，约占牙周膜体积的65%。牙周膜胶原主纤维两端分别连接牙骨质和牙槽骨，可使牙周膜担负持续的咬合力。基质是牙周膜的主要组成部分，其中70%为液体。由于牙周膜生理结构复杂，其生物力学特性也高度复杂。
牙周膜的力学特性因胶原纤维所在部位、功能、排列方向不同而存在区域特异性。在正畸载荷作用下，牙周膜的应力分布发生改变，导致牙周膜内胶原纤维紊乱和重构，尤其是在正畸牙移动过程中应力集中于根尖区，未成熟的Ⅲ型胶原纤维和炎症增加影响了其力学特性[2]。通过原子力显微镜观察发现牙周膜的胶原网络分布呈密集或稀疏网络片状。受压侧的牙周膜胶原纤维网格稀疏；张力侧的胶原纤维网状密集，且牙周膜作为非均匀的实体，随着可变载荷状态变化，纤维组织会在最优方向提供内力并发育至最佳状态[3,4,5]。Hirashima等[6,7,8]通过聚焦离子束/扫描电子显微镜重建牙周膜的三维超微结构，进一步验证了牙周膜的胶原束并非单一的绳状结构，而呈多分枝结构，胶原束的水平纤维区域是一个较厚的、排列紧密的网状结构，胶原束的斜向纤维和顶端纤维呈链状，形成一个"弹弓状"结构，有助于牙齿固定于牙槽骨内。
牙周膜将正畸力和咀嚼力传递至牙槽骨，从机械角度来看，除了胶原纤维参与传递作用力，牙周膜的液体成分，如牙周膜的基质和血管的液体成分也通过静水压力抵抗施加的力，液相的缓冲行为使得牙周膜具有非线性、时间相关性行为。凝胶状的基质组织使牙周膜表现出可压缩、超弹性的特性，以黏弹性、非线性方式承担应力，其特征为先产生瞬时移位，继而发生蠕变式位移。然而，由于牙周膜结构的复杂性以及实验力学的局限性，难以获得真实的人体牙周膜应力/应变比值，现有的研究多采用数值仿真分析方法，因此牙周膜的生物力学响应及本构模型是牙周膜应力/应变分析的关键因素。
牙周膜的生物力学响应主要包含以下几个方面：①静态响应，即短期或瞬时响应，通常以弹性材料模型模拟。②动态响应，即所谓的长期或延迟响应，通常引起软组织液体成分与时间相关的黏弹特性或渗透特性。③容积响应，由压缩能力或泊松系数决定，是体积变化过程中抗体积变化的能力。关于牙周膜力学响应分析和本构模型的数值模拟，早期研究主要假设牙周膜弹性模量为常量，多采用线弹性模型，弹性模量值范围0.01~1 750 MPa[9]，但牙周膜具有各向异性、非线性特性、应力松弛等特点。根据牙周膜的生物力学特性及牙周膜实验应力/应变关系[10,11,12,13,14]，研究者提出了黏弹性模型[15,16,17,18,19,20,21,22,23]、超弹性模型[24,25,26,27]、黏-超弹性模型[28,29,30]、多相耦合模型[31,32,33,34]、多孔纤维弹性模型[35,36,37,38,39]等。
牙周膜的细胞和胶原纤维束间隙含有大量的组织液，这种充满液体的连续多孔结构使牙周膜存在黏弹性力学性质，具有非线性的应力/应变关系，包括弹性滞后、蠕变和应力松弛等。牙周膜作为一种黏弹性材料，在载荷下的力学响应与时间相关，表现为瞬时响应和随时间变化响应，在很短时间内，黏性特征可忽略，表现为瞬时弹性；随时间变化的特征用松弛函数表示，如蠕动、应力松弛、滞后作用等。当正畸力首先作用于牙齿，牙周膜瞬时快速位移期间的初始阶段仅持续几秒钟，牙周膜表现出瞬态黏弹性蠕变响应。然后在3~7 min内稳定，当牙周膜被压缩至最大程度或施加力与牙周膜组织抵抗力处于平衡阶段时表现为应力松弛，应力松弛为牙槽骨提供了长期的载荷，引起牙槽骨重建，从而导致牙齿的移动[15]。Natali等[16]提出了采用非线性黏弹性本构模型来描述牙周膜的弛豫现象。Wang等[17]认为牙周膜的液体成分为主要的蠕动因素，黏弹性能主要由液体和血管系统体积变化所引起，拉-压黏弹性模型更符合牙周膜的生物力学行为。近年来有学者先后通过广义的Maxwell模型构建黏弹性模型，在0.01~100 Hz频率范围测试牙周膜在拉伸和压缩状态下的黏弹性特性，描述其短期和长期响应，结果发现牙周膜损失因子在压缩过程中比在拉伸过程中大，验证了液相在压缩载荷响应中发挥了重要作用[18,19]。Zhou等[20]通过进行牙周膜轴向剪切实验发现牙周膜的蠕变柔量不收敛，提出了牙周膜黏弹性流体本构模型，进一步肯定了液体对牙周膜蠕变的影响。东南大学及南京医科大学课题组先后研究了牙周膜的黏弹性，结果发现其在0.5~10 Hz范围内随频率和牙齿位置而改变，在动态压缩载荷下验证了牙周膜黏弹性与频率相关[21,22,23]。
黏弹性模型主要有弹性元件与黏性元件串联的Maxwell模型以及弹性元件和黏性元件并联的Kelvin模型。以伯格斯模型（Burgers model）[20]为例，其由一个Kelvin模型串联一个Maxwell模型，伯格斯模型的本构模型如下：
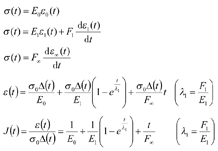
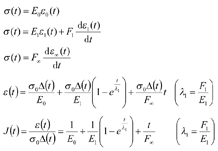
式中：σ（t）、ε（t）和J（t）分别为伯格斯模型系统的总应力、蠕变应变和蠕变柔量，ε0（t）、ε1（t）和ε∞（t）分别为瞬时弹性元件、Kelvin元件和阻尼器的应变，E0、E1、F1、F∞分别为对应的系数，λ1为Kelvin模型蠕变推迟时间。
超弹性模型认为牙周膜可作为包含许多可折叠孔洞的超弹性基质，压应力可视为液体流动的相连系统，牙周膜对压应力的力学响应激活其基质成分和血管，该模型解释了牙周膜的非线性行为、大变形、各向异性特征[24]。牙周膜的应力-应变关系曲线表现为指数形式，即初始应力随应变平缓变化，当应变达到一定程度时，应力随应变迅速增加，由此提出了指数形式的超弹性模型来表示牙周膜的瞬时超弹性，如Mooney-Rivlin模型[25]、V-W模型[26]、Ogden模型[27]等。传统的超弹性模型通常需要很多材料参数来呈现才能准确描述非线性力学行为，而V-W指数式超弹性模型具有较高的精度和较少的参数，便于预测牙周膜的机械响应。
超弹性本构方程包含了生物软组织的基本力学特征：非线性行为、大变形、各向异性拉伸/压缩行为以及纤维特征。以指数超弹性模型为例，将可压缩材料应变能函数分解为等容应变能和体积应变能两部分[26]：
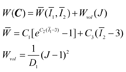
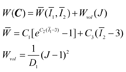
式中：
和Wvol分别代表指数应变能函数和各向同性体积应变能函数，C为右柯西-格林变形张量，
和
为等体积右柯西-格林变形张量的主不变量，J为变形梯度张量的雅可比行列式，D1为体积模量的倒数，C1、C2和C3为材料模型参数。
牙周膜可作为双相介质材料，由胶原纤维固相和组织液液相构成。牙周膜纤维固相及其液相间的黏性行为相互作用，力学响应复杂。固-液双相模型与超黏弹性模型[28,29,30]原理类似，耦合牙周膜基质中液相成分响应迟滞造成的黏性阻尼性质以及固相弹性纤维成分随应力变化产生的弹性性质。
牙周膜受到拉应力时，基质中充满了来自骨组织的液体；当牙周膜受到压应力时，液流方向则为从牙周膜到骨组织。牙周膜的固-液相相互作用的存在使得固相可抵抗拉应力，液相可承受压应力，因此双相材料能更好地模拟牙周膜的微观行为以及时间依赖性和大变形行为[31]。在压应力下，力学响应为黏性行为，牙周膜显示出假塑黏性特征，其本质上是由于纤维基质与组织非约束流体成分的相互作用导致的。早期研究以假塑性、时间相关的本构方程描述该力学响应仅适用于压应力下力学响应部分[32]。拉应力响应由牙周膜不同结构改性决定，牙周膜对拉应力的力学响应是基于纤维结缔组织的牵拉作用，对压应力的响应是激活混合液体如基质成分和血管等的分离。Bergomi等[33]提出采用水应力耦合模型将牙周膜基质成分视为液体，固体成分以线弹性模型、超弹泡沫模型等模拟，将压应力视为液体可流动通过的相互连接的孔隙系统，将牙周膜视为包含很多可折叠孔洞的超弹性基质，在压应力作用下，液体通过孔隙受到挤压后迁移至牙周膜的连接区域或邻近的牙槽骨内。
牙周膜固-液双相模型将其模拟为均匀的混合固体和流体，更适合模拟人牙周膜研究其生物力学特性，以Favino等[34]提出的固-液双相模型方程为例：
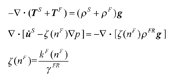
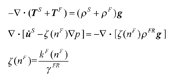
式中：ραg为体积力，Tα为相应的柯西应力张量，
为固相位移，ζ（nF）为达西变形相关参数，p为有效流体压力，kF（nF）为渗透性对流体比的影响，γFR为有效的流体固体比重。
牙周膜是一种复杂的胶原纤维增强复合材料。牙周膜中胶原纤维有明显的空间优先取向，其分布具有独特方向。根据机械条件进行优化或组织结构重组，胶原纤维抵抗非线性拉应力，富含液体的基质成分抵抗压应力，牙周膜中的纤维影响牙齿旋转中心与阻抗中心，从而影响正畸牙移动[35]。
胶原纤维的弹性特性和流体相的阻尼特性是牙周膜的非线性和时变特性的主要原因，牙周膜对拉应力的力学响应是基于其纤维结缔组织的牵拉作用。McCormack等[36,37]提出了牵拉纤维假说，认为经典的正畸牙移动张-压应力学说未反映牙周膜中弹性纤维的作用，在压力侧，牙周膜中的纤维成分受压，对牙槽骨力的传递作用微乎其微；而在拉力侧，胶原纤维与牙周膜的各向异性、组织的应力-应变行为有关，纤维经过牵拉将正畸力传递至牙槽骨。因此，采用具有拉应力的杆单元模拟纤维成分和固体单元模拟基质成分相结合的方法，构建牙周膜纤维模型模拟正畸牙移动，较无纤维模型更能准确模拟牙周膜的特性，但牙周膜胶原纤维的有限元模拟增大了建模和计算的复杂度。Ortún-Terrazas等[38,39]认为牙周膜是一种非线性、时间相关、多相位、多孔弹性的纤维增强结构，针对牙周膜的多孔纤维特性，构建了横观各向同性的多孔纤维弹性模型，结果发现在压应力下，由于牙周膜的体积模量取决于间隙流体的排出能力，其力学响应受其多孔性能影响较大；在拉应力下，其力学响应主要取决于沿载荷方向运动的胶原纤维。
从生物力学上讲，牙周膜富含高度结构化的胶原网络，可视为多孔血管化固体复合生物材料。由于其多孔结构、液相和高血管特性，牙周膜可通过横观各向同性纤维多孔超弹性应变能函数表示[38,39]，具体如下：
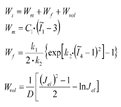
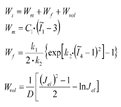
式中：Wm、Wf和Wvol分别为超弹性基质应变能、纤维增强应变能和体积应变能，C1为基质参数，k1和k2为胶原纤维参数，D为体积模量的倒数，Jel=detF，
为修改后的主不变量。
所有作者均声明不存在利益冲突
