
介绍亚群治疗效果模式图(STEPP)的基本原理、应用场景与主要步骤,梳理将其与倾向性评分匹配(PSM)联合应用在队列研究数据中的理论基础,旨在将STEPP应用到暴露与结局风险关联的异质性分析中。通过模拟案例“不同输液导管类型的肿瘤患者发生静脉血栓栓塞(VTE)风险的队列研究”展示如何将PSM与STEPP在队列研究数据中联合应用,得出亚群中经外周置入中心静脉导管组和中心静脉导管组发生VTE的绝对风险值和相对风险值,以及亚群间的异质性分析结果,并对PSM与STEPP联合应用的局限性和研究前景进行讨论,为实际应用提供参考。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
亚群治疗效果模式图(STEPP)是一种可用来探究研究对象不同亚群间治疗效果异质性的探索性图形工具,多用于随机临床试验(RCT)数据的分析[1, 2, 3]。在RCT中,当存在一个影响结局发生风险的连续性协变量时,根据该协变量将研究对象划分为多个有部分重叠的亚群后分别进行相应的统计分析,得到各亚群中试验组与对照组治疗效果的绝对值或相对值等,进一步发现从干预措施获益较大或较小的亚群以及干预措施与该协变量的交互作用[1,4]。据此,对于队列研究,当同样存在一个影响结局发生风险或与暴露有交互作用的连续性协变量时,若探究不同亚群中暴露与结局关联的异质性,也可尝试使用STEPP分析。但要注意的是,RCT中试验组与对照组的基线特征理论上是均衡可比的,队列研究中基线特征在暴露组与对照组间的分布或构成可能不均衡,即可能存在较多混杂因素。而倾向性评分匹配(PSM)是队列研究数据分析中常用的混杂控制方法,可达到“类随机化”的效果[5]。本研究在模拟数据中尝试将PSM与STEPP联合,进行队列研究中暴露与结局关联的异质性分析。
1. 基本原理:在对RCT数据进行分析时,通常会使用各数据集中全部研究对象进行统计分析和推断,如全分析集和依从方案集。当存在影响结局的基线特征(协变量)时,研究对象的疗效会随着该基线特征的变化而有所变化,研究对象间便存在疗效的异质性,如银屑病患者的疗效会受到基线期银屑病面积及严重指数的影响[6]。此时,若依然使用基于全集得到的结果对每个研究对象的疗效进行推论,是不合适的[7]。通常,若考虑疗效在不同特征研究对象中有异质性,或考虑干预措施与某基线特征存在交互作用时,可进行亚组分析或在回归分析中增加两者的交互项。而对于亚组分析,存在两个主要的问题:一是多重检验增加了Ⅰ类错误,二是亚组的样本量减小或统计把握度不足[1]。另外,当协变量是连续性变量时,也给亚组分析带来了挑战;而对此通常的做法是进行变量转化,即将连续性变量根据某种标准转化成定性变量(分类变量)。但这种变量转化在改变变量类型的同时,也损失了变量信息,可能会使得分析结果不够精确。
针对上述问题,Bonetti和Gelber[2]提出了采用STEPP探究治疗效果在亚群中的异质性以及协变量与治疗措施的交互作用。其中,亚群是根据连续性或有序多分类协变量进行划分的,且相邻的亚群间有大部分研究对象是重叠的。如此,便做到了根据连续性或有序多分类协变量进行亚群划分,研究者在进行亚群间异质性分析的同时也可更容易地发现受益较大或较小的亚群。相比互不重叠的亚组,在有重叠的亚群中探究疗效的异质性更符合真实世界的需求,也提高了估计的精准性。
2. 分析步骤:
(1)在RCT数据中的分析步骤:在对RCT数据分析时,STEPP的实现主要包括4个步骤[1,7]。
划分亚群:设定亚群的例数和相邻亚群重叠的例数,根据连续性协变量将研究对象分为多个有重叠的亚群。其中,亚群划分的方式主要分为滑窗式和拖尾式。见图1。
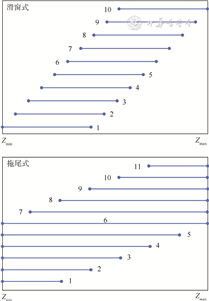

注:Zmin和Zmax分别代表连续性协变量的最小值和最大值
估计治疗效果:根据结局变量的类型,采用相应的统计分析方法(如二分类logistic回归、Poisson回归、Cox比例风险回归模型、竞争风险模型等)在每个亚群内估计治疗效果,如试验组与对照组的结局发生率/累积发生率、累积发生率差值(RD)、RR或风险比(HR)等。
推断:计算每个亚群治疗效果的CI,并构建CI带;同时,通过置换检验对各个亚群治疗效果是否相等进行假设检验。
绘制统计图:以各个亚群协变量的中位数为横轴,以对应的亚群治疗效果为纵轴绘制统计图。例如,因变量为时间-事件变量时,可对各亚群中结局的累积发生率、RD(95%CI)、HR值(95%CI)绘制折线图。
(2)在队列研究数据中的分析步骤:推广至队列研究中,因为(可疑)混杂因素的存在,所以需要在进行STEPP前控制混杂因素。PSM可达到暴露组与对照组“类随机化”的效果(事后随机化),实现控制队列研究中已观察到的(可疑)混杂因素的目的[8]。因此,考虑将PSM与STEPP连用,以探究队列研究中暴露与结局关联的异质性。该过程主要包括2个部分:
PSM:基于相应的统计学分析(如暴露组与对照组基线特征的差异性比较)或因果有向无环图[9]等确定(可疑)混杂因素;之后,将(可疑)混杂因素作为PSM的匹配变量进行匹配;经过PSM,可得到暴露组与对照组基线特征均衡可比的匹配数据集。对于匹配的方式,可选择贪婪匹配或最优匹配。一般情况下,常采用贪婪匹配中的最近邻匹配或卡钳匹配。当使用卡钳匹配时,需注意设置合适的卡钳值[8]。另外,根据暴露组与对照组的例数和倾向性评分的重叠情况,可设置合适的匹配比例,如1∶1、1∶2。
STEPP分析:基于匹配数据,根据感兴趣的连续性协变量进行亚群划分,如年龄、疾病严重程度评分等;估计暴露组和对照组的结局发生率/累积发生率(如发病率、累积死亡率等)或结局指标绝对值(如中医症候积分、匹兹堡睡眠质量指数量表等)、RD或绝对值的差值、RR/HR等;根据协变量对各亚群的治疗效果指标进行置换检验,分析亚群间治疗效果是否相等;根据治疗效果的效应值及其CI绘制统计图。
1. 案例介绍:静脉血栓栓塞(VTE)是肿瘤患者常出现的并发症。有研究表明,输液导管会增加VTE的风险,即可导致输液导管相关静脉血栓形成[10]。在输液导管中,中心静脉通路装置较为常用,包括经外周置入中心静脉导管(PICC)、中心静脉导管(CVC)和输液港。
根据既往文献报道[11, 12],本研究模拟了采用PICC或CVC的肿瘤患者发生VTE风险的队列研究数据。研究对象在进入队列时均无VTE,根据采用的输液导管类型分为PICC组和CVC组,收集基线期患者信息(人口学特征、生活行为方式、合并症、治疗情况和实验室检查指标等),随访180 d观察两组患者的VTE发生率。考虑到年龄是很多疾病的影响因素,本研究以年龄为协变量,基于PSM后的数据进行STEPP分析,探究不同年龄亚群中两组患者VTE风险的异质性。同时,在匹配后的全部研究对象中,采用Cox比例风险回归模型分析输液导管类型对VTE发生风险的影响,与STEPP结果进行对比。在STEPP分析中,设置亚群例数为1 000例,相邻亚群重叠的例数为900例,亚群划分方式为滑窗式。统计分析与绘图均通过R 4.2.0软件和MatchIt、stepp、survival、ggplot2等程序包以及梦特云统计平台(https://mengte.pro)完成,设置假设检验水准α=0.05。
2. 案例结果:共纳入研究对象3 414例,其中PICC组839例,CVC组2 575例。对两组研究对象的基线特征进行比较,结果表明,年龄、性别、是否化疗、肿瘤分期、是否有糖尿病、是否使用激素、血栓史、血小板计数、血红蛋白和纤维蛋白原在两组间的差异有统计学意义(均P<0.05);将上述有差异的基线特征作为PSM的匹配变量,采用卡钳匹配(卡钳值为0.1)进行1∶2匹配。经过PSM,PICC组与CVC组基线特征的差异无统计学意义(除高血压外),且标准化均差(SMD)均<0.100,可认为两组已观察的基线特征均衡可比。见表1。
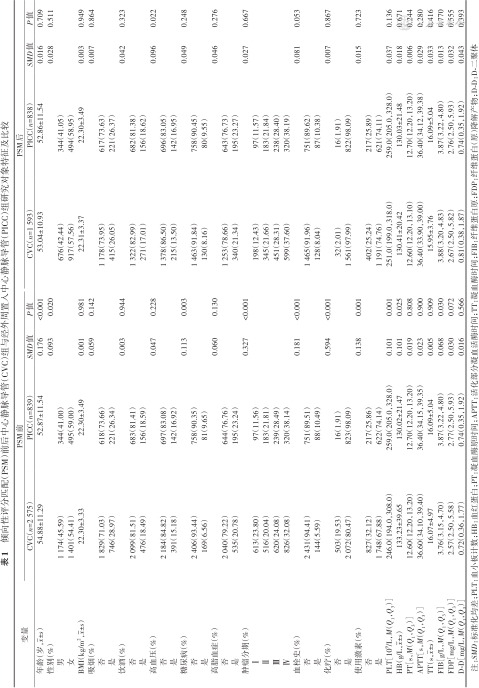
倾向性评分匹配(PSM)前后中心静脉导管(CVC)组与经外周置入中心静脉导管(PICC)组研究对象特征及比较
倾向性评分匹配(PSM)前后中心静脉导管(CVC)组与经外周置入中心静脉导管(PICC)组研究对象特征及比较
| 变量 | PSM前 | PSM后 | ||||||
|---|---|---|---|---|---|---|---|---|
| CVC(n=2 575) | PICC(n=839) | SMD值 | P值 | CVC(n=1 593) | PICC(n=838) | SMD值 | P值 | |
| 年龄(岁,x±s) | 54.88±11.29 | 52.87±11.54 | 0.176 | <0.001 | 53.04±10.93 | 52.86±11.54 | 0.016 | 0.709 |
| 性别(%) | 0.093 | 0.020 | 0.028 | 0.511 | ||||
| 男 | 1 174(45.59) | 344(41.00) | 676(42.44) | 344(41.05) | ||||
| 女 | 1 401(54.41) | 495(59.00) | 917(57.56) | 494(58.95) | ||||
| BMI(kg/m2,x±s) | 22.30±3.33 | 22.30±3.49 | 0.001 | 0.981 | 22.31±3.37 | 22.30±3.49 | 0.003 | 0.949 |
| 吸烟(%) | 0.059 | 0.142 | 0.007 | 0.864 | ||||
| 否 | 1 829(71.03) | 618(73.66) | 1 178(73.95) | 617(73.63) | ||||
| 是 | 746(28.97) | 221(26.34) | 415(26.05) | 221(26.37) | ||||
| 饮酒(%) | 0.003 | 0.944 | 0.042 | 0.323 | ||||
| 否 | 2 099(81.51) | 683(81.41) | 1 322(82.99) | 682(81.38) | ||||
| 是 | 476(18.49) | 156(18.59) | 271(17.01) | 156(18.62) | ||||
| 高血压(%) | 0.047 | 0.228 | 0.096 | 0.022 | ||||
| 否 | 2 184(84.82) | 697(83.08) | 1 378(86.50) | 696(83.05) | ||||
| 是 | 391(15.18) | 142(16.92) | 215(13.50) | 142(16.95) | ||||
| 糖尿病(%) | 0.113 | 0.003 | 0.049 | 0.248 | ||||
| 否 | 2 406(93.44) | 758(90.35) | 1 463(91.84) | 758(90.45) | ||||
| 是 | 169(6.56) | 81(9.65) | 130(8.16) | 80(9.55) | ||||
| 高脂血症(%) | 0.060 | 0.130 | 0.046 | 0.276 | ||||
| 否 | 2 040(79.22) | 644(76.76) | 1 253(78.66) | 643(76.73) | ||||
| 是 | 535(20.78) | 195(23.24) | 340(21.34) | 195(23.27) | ||||
| 肿瘤分期(%) | 0.327 | <0.001 | 0.027 | 0.667 | ||||
| Ⅰ | 613(23.80) | 97(11.56) | 198(12.43) | 97(11.57) | ||||
| Ⅱ | 516(20.04) | 183(21.81) | 345(21.66) | 183(21.84) | ||||
| Ⅲ | 620(24.08) | 239(28.49) | 451(28.31) | 238(28.40) | ||||
| Ⅳ | 826(32.08) | 320(38.14) | 599(37.60) | 320(38.19) | ||||
| 血栓史(%) | 0.181 | <0.001 | 0.081 | 0.053 | ||||
| 否 | 2 431(94.41) | 751(89.51) | 1 465(91.96) | 751(89.62) | ||||
| 是 | 144(5.59) | 88(10.49) | 128(8.04) | 87(10.38) | ||||
| 化疗(%) | 0.594 | <0.001 | 0.007 | 0.867 | ||||
| 否 | 503(19.53) | 16(1.91) | 32(2.01) | 16(1.91) | ||||
| 是 | 2 072(80.47) | 823(98.09) | 1 561(97.99) | 822(98.09) | ||||
| 使用激素(%) | 0.138 | 0.001 | 0.015 | 0.723 | ||||
| 否 | 827(32.12) | 217(25.86) | 402(25.24) | 217(25.89) | ||||
| 是 | 1 748(67.88) | 622(74.14) | 1 191(74.76) | 621(74.11) | ||||
| PLT[109/L,M(Q1,Q3)] | 246.0(194.0,308.0) | 259.0(205.0,328.0) | 0.101 | 0.001 | 251.0(199.0,318.0) | 259.0(205.0,328.0) | 0.037 | 0.136 |
| HB(g/L,x±s) | 133.23±39.65 | 130.02±21.47 | 0.101 | 0.025 | 130.41±20.42 | 130.03±21.48 | 0.018 | 0.671 |
| PT[s,M(Q1,Q3)] | 12.60(12.20,13.20) | 12.70(12.20,13.20) | 0.019 | 0.808 | 12.60(12.20,13.10) | 12.70(12.20,13.20) | 0.006 | 0.244 |
| APTT[s,M(Q1,Q3)] | 36.60(34.10,39.40) | 36.40(34.15,39.35) | 0.023 | 0.900 | 36.40(33.90,39.00) | 36.40(34.12,39.38) | 0.029 | 0.280 |
| TT(s,x±s) | 16.07±4.97 | 16.09±5.04 | 0.005 | 0.909 | 15.95±3.76 | 16.09±5.04 | 0.033 | 0.416 |
| FIB[g/L,M(Q1,Q3)] | 3.76(3.15,4.70) | 3.87(3.22,4.80) | 0.068 | 0.030 | 3.88(3.20,4.83) | 3.87(3.22,4.80) | 0.013 | 0.770 |
| FDP[mg/L,M(Q1,Q3)] | 2.57(2.50,5.58) | 2.77(2.50,5.93) | 0.030 | 0.072 | 2.67(2.50,5.82) | 2.76(2.50,5.93) | 0.032 | 0.555 |
| D-D[mg/L,M(Q1,Q3)] | 0.72(0.36,1.77) | 0.74(0.35,1.92) | 0.016 | 0.566 | 0.81(0.38,1.87) | 0.74(0.35,1.92) | 0.043 | 0.393 |
注:SMD:标准化均差;PLT:血小板计数;HB:血红蛋白;PT:凝血酶原时间;APTT:活化部分凝血活酶时间;TT:凝血酶时间;FIB:纤维蛋白原;FDP:纤维蛋白(原)降解产物;D-D:D-二聚体
STEEP分析中共划分了9个亚群,在各亚群中两组的累积发生率均呈现先下降后上升的趋势,且CVC组的VTE累积发生率低于PICC组(表2,图2),但置换检验结果显示各亚群间的差异无统计学意义(置换检验P=0.950)。
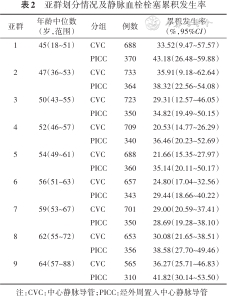
亚群划分情况及静脉血栓栓塞累积发生率
亚群划分情况及静脉血栓栓塞累积发生率
| 亚群 | 年龄中位数(岁,范围) | 分组 | 例数 | 累积发生率 (%,95%CI) |
|---|---|---|---|---|
| 1 | 45(18~51) | CVC | 688 | 33.52(9.47~57.57) |
| PICC | 370 | 43.18(26.48~59.88) | ||
| 2 | 47(36~53) | CVC | 733 | 35.91(9.18~62.64) |
| PICC | 364 | 38.32(22.56~54.08) | ||
| 3 | 50(43~55) | CVC | 723 | 29.31(12.57~46.05) |
| PICC | 350 | 34.82(19.49~50.15) | ||
| 4 | 52(46~57) | CVC | 709 | 20.53(14.77~26.29) |
| PICC | 340 | 36.46(20.23~52.69) | ||
| 5 | 54(49~61) | CVC | 688 | 21.66(15.35~27.97) |
| PICC | 360 | 35.14(20.11~50.17) | ||
| 6 | 56(51~63) | CVC | 657 | 24.80(17.04~32.56) |
| PICC | 343 | 29.44(18.66~40.22) | ||
| 7 | 59(53~67) | CVC | 701 | 29.00(20.59~37.41) |
| PICC | 350 | 28.69(19.28~38.10) | ||
| 8 | 62(55~72) | CVC | 653 | 30.08(21.65~38.51) |
| PICC | 356 | 38.58(27.70~49.46) | ||
| 9 | 64(57~88) | CVC | 565 | 36.27(25.71~46.83) |
| PICC | 310 | 41.82(30.14~53.50) |
注:CVC:中心静脉导管;PICC:经外周置入中心静脉导管

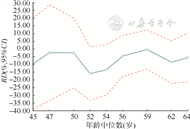
各亚群的RD呈现出双峰趋势,在第4亚群中两组RD最大(RD=-15.93%,95%CI:-33.16%~1.30%)(表3,图3),但亚群间的差异无统计学意义(置换检验P=0.950)。
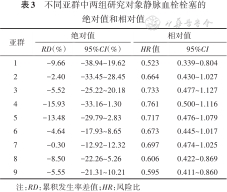
不同亚群中两组研究对象静脉血栓栓塞的绝对值和相对值
不同亚群中两组研究对象静脉血栓栓塞的绝对值和相对值
| 亚群 | 绝对值 | 相对值 | ||
|---|---|---|---|---|
| RD(%) | 95%CI(%) | HR值 | 95%CI | |
| 1 | -9.66 | -38.94~19.62 | 0.523 | 0.339~0.804 |
| 2 | -2.40 | -33.45~28.45 | 0.664 | 0.430~1.027 |
| 3 | -5.52 | -25.22~20.18 | 0.733 | 0.477~1.127 |
| 4 | -15.93 | -33.16~1.30 | 0.761 | 0.500~1.116 |
| 5 | -13.48 | -29.79~2.83 | 0.717 | 0.476~1.079 |
| 6 | -4.64 | -17.93~8.65 | 0.673 | 0.445~1.017 |
| 7 | -0.30 | -12.92~12.32 | 0.697 | 0.474~1.025 |
| 8 | -8.50 | -22.26~5.26 | 0.606 | 0.422~0.869 |
| 9 | -5.55 | -21.31~10.21 | 0.595 | 0.411~0.860 |
注:RD:累积发生率差值;HR:风险比

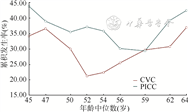
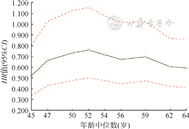
与PICC组相比,各亚群中CVC组的HR值呈现先上升后下降的趋势,各亚群间HR值的差异有统计学意义(置换检验P<0.001);在第1亚群、第8亚群和第9亚群中,CVC组发生VTE的风险低于PICC组,而其他亚群内输液管类型与VTE风险无统计学关联(均P>0.05)。表明在不同年龄段的亚群中,CVC组相比PICC组发生VTE的风险不同,亚群间具有异质性(表3,图4)。

在匹配后的全部研究对象中分析CVC相比PICC发生VTE的风险,结果显示,CVC组发生VTE的风险比PICC组低0.384倍(HR=0.616,95%CI:0.482~0.787),有统计学关联(P<0.001);当考虑年龄与输液管类型的交互作用时,结果显示,CVC组发生VTE的风险比PICC组低0.480倍(HR=0.520,95%CI:0.140~1.938),但无统计学关联(P=0.330)。见表4。与STEPP分析的结果相比可知,无论是否考虑暴露因素与连续性协变量的交互作用,以全部观测数据得到的分析结果并不适用于全部的亚群(不同年龄组的研究对象),未能考虑和体现风险的异质性。而STEPP分析能更加精细化分析,以连续性变量为亚群划分依据,得到不同亚群对应的暴露与结局风险的关联及强度,实现异质性分析。
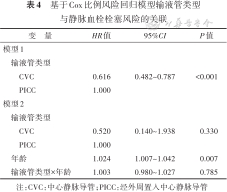
基于Cox比例风险回归模型输液管类型与静脉血栓栓塞风险的关联
基于Cox比例风险回归模型输液管类型与静脉血栓栓塞风险的关联
| 变 量 | HR值 | 95%CI | P值 |
|---|---|---|---|
| 模型1 | |||
| 输液管类型 | |||
| CVC | 0.616 | 0.482~0.787 | <0.001 |
| PICC | 1.000 | ||
| 模型2 | |||
| 输液管类型 | |||
| CVC | 0.520 | 0.140~1.938 | 0.330 |
| PICC | 1.000 | ||
| 年龄 | 1.024 | 1.007~1.042 | 0.007 |
| 输液管类型×年龄 | 1.003 | 0.980~1.027 | 0.785 |
注:CVC:中心静脉导管;PICC:经外周置入中心静脉导管
目前,STEPP分析主要应用于RCT数据的事前或事后分析,尤其是肿瘤相关的RCT[13, 14, 15, 16]。本研究将PSM与STEPP分析相结合,尝试基于队列研究数据分析暴露与结局风险关联在研究对象中的异质性。即通过PSM实现暴露组与对照组研究对象的事后随机化,再基于匹配后的研究对象进行STEPP分析。结果表明,相比在全部研究对象中进行分析得到的暴露与结局风险的关联/关联强度,STEPP实现了暴露与结局风险关联/关联强度的异质性分析。然而,在本研究中虽然第1亚群(年龄18~51岁)、第8亚群(年龄55~72岁)和第9亚群(年龄57~88岁)中CVC组发生VTE的风险较低,但并未真正发现获益最大或最小的亚群。广大研究者在实际应用时,折线图中如能出现峰值或谷值,且有统计学关联,那么进行异质性分析的同时可获知最大或最小获益组/风险组。
本研究是以生存数据为例,在亚群中基于Kaplan-Meier分析和Cox比例风险回归模型进行数据分析。但STEPP分析不仅适用于生存数据,也适用于服从Gaussian分布、二项分布、Poisson分布的结局变量以及存在竞争事件的时间-事件变量,所采用的分别是广义线性模型(分布函数分别为Gaussian、Binomial和Poisson)和竞争风险模型[7]。针对所分析的因变量类型而言,其使用场景便会更加广泛,比如Cao等[17]采用STEPP从卫生经济学角度,探究依据基线风险进行分层治疗和“一刀切”的优劣。
由于随机分组(如简单随机化、分层随机化等)可以实现试验组和对照组基线特征的均衡化,在RCT数据中应用STEPP分析时可不考虑混杂因素带来的混杂偏倚,直接分析干预措施在不同亚群中的治疗效果。在观察性研究中可能存在大量的已观察到或未观察到的混杂因素,若要基于STEPP探究不同亚群中暴露与结局的关联及其强度,需要先控制混杂偏倚。而PSM虽然可以实现类随机化,但能控制的仅是已观察到的混杂偏倚,不能控制未观察到的混杂[18]。而且,经过PSM后样本量会有所损失,降低了统计分析效能[5]。另外,在使用PSM时,应注意其适用条件,如暴露组与对照组的倾向性评分有一定的重叠[5]。上述主要是PSM所带来的局限性,而STEPP自身也有一定的局限性。第一,在划分亚群时需要预先指定亚群例数和重叠例数,当这两个参数变化时,所形成的亚群数以及结果可能会有所不同。对此,可设置多组参数进行敏感性分析[4],或者划分亚群时设定每个亚群中结局事件不低于20例[3],从而确保分析结果的稳健性。另外,根据本研究的经验,建议在划分亚群时要使协变量的中位数(范围)不重叠,以确保可以根据一系列亚群的分析结果进行异质性分析。同时,根据总体样本量划分适宜数量的亚群,尽量保证每个亚群有足够的样本量;当重叠的例数越大时,所分的亚群数量越多,也便于更加细致地分析协变量的变化对结局的影响。第二,绝对效应或相对效应指标的选择可影响亚群间是否存在异质性的推断,如本研究中CVC组和PICC组的事件累积发生率、RD在亚群间的异质性无统计学意义,而HR值在亚群间的异质性有统计学意义。因此,建议根据研究目的选择合适的效应指标,但不反对同时使用多个或多种效应指标更加全面地报告与讨论。
虽然存在一定的局限性,但相比将基于全部研究对象的分析结果应用于不同特征(如不同年龄或风险分层)的患者,或进行常规的亚组分析,PSM与STEPP相结合的优势依然不可忽视。
若抛开既有的用于STEPP分析的R语言程序包,仅依据STEPP原理与步骤进行分析的方法组合,那么基于队列研究数据分析暴露与结局风险关联的异质性时,所采用的分析思路便可多样化。例如,在每个亚群内分别拟合多因素回归模型以校正混杂因素[19],得到校正后关联强度的点估计值及其95%CI,然后将各亚群的关联强度进行置换检验,并绘制成统计图(折线图、柱状图等);在每个亚群内使用逆概率加权法进行分析,可得到每个亚群中暴露组与对照组的结局发生率及RD等;在每个亚群中使用工具变量法,得到关联强度的点估计值及其95%CI[5]。
综上所述,基于PSM与STEPP的思想将两者相结合,可在队列研究数据中尝试分析暴露与结局风险的关联在不同亚群中的异质性,实现将STEPP分析应用到队列研究中的目的。
王威, 于茜, 胡馨茹, 等. 基于倾向性评分匹配和亚群治疗效果模式图队列研究暴露与结局关联的异质性分析[J]. 中华流行病学杂志, 2024, 45(5): 748-754. DOI: 10.3760/cma.j.cn112338-20231121-00303.
Wang W, Yu Q, Hu XR, et al. Heterogeneous analysis on association between exposure and outcome in cohort studies:based on propensity score matching and subpopulation treatment effect pattern plot[J]. Chin J Epidemiol, 2024, 45(5):748-754. DOI: 10.3760/cma.j.cn112338-20231121-00303.
所有作者声明无利益冲突



























