
本讲概述统计描述、统计推断、统计模型、统计模拟等统计分析的基本方法。
版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
本讲概述统计描述、统计推断、统计模型、统计模拟等统计分析的基本方法。
统计描述是指通过图表或数学方法,对抽样获得的样本数据资料进行整理、分析,并对数据的分布状态、数字特征和随机变量之间关系进行估计和描述的方法。统计描述一般包括集中趋势描述、离散趋势描述、相关程度描述和统计图表四部分。计量资料和计数资料的统计描述方法见表1。

计量资料和计数资料的统计描述方法
计量资料和计数资料的统计描述方法
| 统计描述方法 | 计量资料 | 计数资料 |
|---|---|---|
| 集中趋势描述 | 算术平均数(正态分布资料)、几何平均数(对数正态分布资料)、中位数(偏态分布资料) | 平均率(总体率) |
| 离散趋势描述 | 标准差(正态分布资料)、四分位间距(偏态分布资料) | 率的标准误 |
| 相关程度描述 | 积差相关系数 | 秩和相关系数 |
| 统计图表 | 三线统计表、各类统计图 | 三线统计表、各类统计图 |
统计推断是指利用样本数据来推断总体特征的统计方法。统计推断一般包括利用样本信息推断总体特征的参数估计方法和利用样本信息判断对总体的假设是否成立的假设检验方法两部分。计量资料和计数资料的统计推断方法见表2。
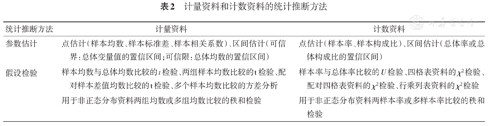
计量资料和计数资料的统计推断方法
计量资料和计数资料的统计推断方法
| 统计推断方法 | 计量资料 | 计数资料 |
|---|---|---|
| 参数估计 | 点估计(样本均数、样本标准差、样本相关系数)、区间估计(可信界:总体变量值的置信区间;可信限:总体均数的置信区间) | 点估计(样本率、样本构成比)、区间估计(总体率或总体构成比的置信区间) |
| 假设检验 | 样本均数与总体均数比较的t检验、两组样本均数比较的t检验、配对样本差值均数比较的t检验、多个样本均数比较的方差分析 | 样本率与总体率比较的U检验、四格表资料的 χ2检验、配对四格表资料的 χ2检验、行乘列表资料的 χ2检验 |
| 用于非正态分布资料两组均数或多组均数比较的秩和检验 | 用于非正态分布资料两样本率或多样本率比较的秩和检验 |
统计模型是指研究变量之间相互影响关系的数学模型,通常是利用抽样研究所得到的样本数据来拟合理论上的数学模型。在医学科研设计中,常用的统计模型包括线性模型(直线回归)、概率模型(Logistic回归)和时间模型(COX回归)[1]。常用统计模型的适用条件和用途见表3。

常用统计模型的适用条件和用途
常用统计模型的适用条件和用途
| 统计模型 | 适用条件 | 用途 |
|---|---|---|
| 线性模型(直线回归) | 要求符合LINE(线性、独立、正态、等方差)的条件。即:Xi与y属于线性相关;观察值彼此独立;观察值围绕回归线的波动服从正态分布;沿回归直线方向总体观察值的方差处处相等。 | 描述变量间相关关系;由一个或多个自变量预测因变量;用确定系数(R2)考核所有自变量对因变量的贡献率;用各自变量的标准回归系数作为综合评价体系的指标权重。 |
| 概率模型(Logistic回归) | 因变量为二分类的分类变量(也可以是多分类的,但是二分类的更为常用,也更加容易解释),或某事件的发生率;自变量为分类变量或连续变量。 | 主要用途为寻找危险因素(寻找某一疾病的危险因素)、预测(不同自变量情况下,某病或某种情况的发生概率)和判别(判断某人属于某病或某种情况的概率有多大)。 |
| 时间模型(COX回归) | 因变量为生存结局和生存时间,自变量为分类变量或连续变量。不要求估计资料的生存分布类型。 | 常用于生存分析,可同时分析众多因素对生存期的影响,能分析带有截尾生存时间的资料。 |
统计模拟是指以特定的统计模型和数学算法为基础,运用计算机软件大量生成合理的仿真样本,并按照研究目的对这些仿真样本重新进行统计分析的过程。统计模拟分为确定型数据模拟和随机型数据模拟两种。统计模拟方法一般包括三个步骤:建立模型、生成样本、参数估计。
陈少科等[2]探索发明了一种称之为模拟随机对照试验方法(simulated randomized controlled trials),简称sRCT。该方法通过对研究对象进行反复模拟随机化分组、借用随机对照试验(randomized controlled trials,RCT)的原理、应用新的统计量,对真实医疗过程中产生的疾病结局变量进行不同治疗方法之间的疗效比较分析,为临床决策提供一种新的证据类型。该方法基于以下原理:针对诊断为同种疾病接受不同治疗的一组患者,采用反复多次模拟随机化分组并根据RCT的统计分析策略进行疗效比较,以拒绝H0的试验频率和不拒绝H0的试验频率之比(odds值)及其95%CI作为判断不同治疗方法间疗效差异的依据。采用计算机模拟的方法获得统计量odds值的分布。对包含结局变量和混杂因素变量的模拟数据库进行随机化分组,对根据符合方案集分析(PP)策略保留下来的样本进行结局变量比较。重复100次随机化分组,并对每次随机化分组后结局变量进行比较,同时也对混杂因素变量的组间均衡性进行分析。计算100次结局变量比较分析结果中拒绝H0与不拒绝H0的比值,即odds值,重复100次odds值的计算过程得到odds值的点估计值及其95%CI。根据样本量(n1=n2=50,100,500和1000)、组间差异的把握度和效应量产生多个模拟数据库,观察分析得到的odds值及其95%CI的一致性和稳定性。同时验证混杂因素在根据PP策略保留下来的样本的组间均衡性。统计模拟结果表明:(1)对不同样本量下疗效有差异数据库分析得到的odds值均>1,odds值及其95%CI均随把握度的增加呈上升趋势;(2)对不同样本量下疗效无差异数据库分析得到的odds值均<1,odds值及其95%CI均随把握度的增加呈下降趋势,二者变化均呈现良好的线性关系;(3)同时验证样本量相等和不相等的情况下,混杂因素组间均衡的概率均>95%。这一模拟随机对照试验方法对模拟数据库分析得到结果的一致性和稳定性高,实现了在均衡混杂因素的基础上,创建了一种用于观察性数据疗效比较研究的新方法。
所有作者均声明不存在利益冲突


























