
本讲概述Meta分析的基本步骤、资料的统计学处理、发表偏倚的识别和控制、Meta分析的软件。
版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
本讲概述Meta分析的基本步骤、资料的统计学处理、发表偏倚的识别和控制、Meta分析的软件。
同一个研究目的所进行的医学研究,全世界范围内可能有几十个、上百个研究对象、设计方案、干预措施、结局变量、样本含量、随访时间等不全相同的研究,研究结果不会完全一致。对这些研究结果进行分析综合的统计方法就是Meta分析。Meta分析的概念可以从广义和狭义两种层次理解:广义的Meta分析指的是一个科学的临床研究活动,指全面收集所有相关研究并逐个进行严格评价筛选和分析,再用定量合成的方法对资料进行统计学处理得出综合结论的整个过程;狭义的Meta分析仅仅是一种单纯的定量合成的统计学方法。目前国内外文献中以广义的概念应用更为普遍[1]。
Meta分析是一类统计方法,用来比较和综合针对同一科学问题所取得的研究结果。比较和综合的结论是否有意义,取决于这些研究是否满足特定的条件。
Meta分析的基本步骤包括:提出问题,制订研究计划;相关文献的检索;确定文献纳入和剔除的标准;资料提取;纳入研究的质量评价;资料的统计学处理;敏感性分析;结果的分析和讨论。
资料的统计学处理包括定义结局变量、异质性检验、模型选择、效应合并值的点估计和区间估计、效应合并值的假设检验5个方面的工作。
对于计数资料的结局变量,可以把 RR(rate ratio,率比)、OR(odds ratio,优势比)、RD (risk difference,率差)定义为结局变量。
为满足正态近似的条件,RR和OR一般取自然对数后用ln(OR)、ln(RR)作为效应值。当OR和RR差别不大时,为计算方便,常用OR代替RR做近似计算。率差也称危险度差值或绝对危险度减少率(ARR),ARR的倒数则称为需要治疗的病人数(NNT),是临床决策的一项有效指标。率差、率比、优势比的参数估计方法见表1。

率差、率比、优势比的参数估计方法
率差、率比、优势比的参数估计方法
| 结局变量 | 参数 | 估计值 | 标准误 |
|---|---|---|---|
| 率差RD | D=P1=P2 | di=p1i-p2i | 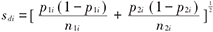 |
| 率比RR | D=P1/P2 | ri=P1i/P2i | 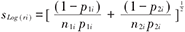 |
| 优势比OR | 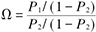 | 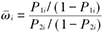 | 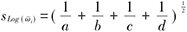 |
对于计量资料的结局变量,可以把均数之差定义为结局变量。为了消除量纲的影响,也可以把标准化均数之差或者相关系数定义为结局变量,作为一种效应尺度。均数之差、方差和标准误的平方估计公式见表2。

均数之差、方差和标准误平方的估计公式
均数之差、方差和标准误平方的估计公式
| 结局变量 | 均数之差Yi |
|---|---|
| 参数 | 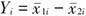 |
| 估计值 | 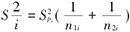 |
| 标准误 | 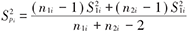 |
异质性检验是指对各原始研究结果之间的变异度进行检验,目的是检验各独立研究结果是否具有可合并性。如果异质性检验结果有统计学意义(P≤0.10),则认为各独立研究结果间异质性较大。
异质性来源包括:(1)临床异质性:如研究对象的特征、诊断、干预措施、对照、研究地点、结局评价等不同;(2)方法学异质性:研究设计与质量不同;(3)统计学异质性:不同研究观察到的效应,其变异度超过了随机误差所致的变异性[2]。
一般采用Q检验方法(χ2值)来进行异质性检验。Q服从自由度为ν=k-1(k为纳入Meta分析的研究个数)的χ2分布。若P≤α (α一般取0.10),则拒绝H0,可认为各研究间异质性大,应采用随机效应模型;若P>α,则不拒绝H0,可认为各研究间具有同质性,应采用固定效应模型。异质性检验的目的是考核各个独立研究的效应值之间是否具有同质性(homogeneity)。
Meta分析有两类模型可供选择:一种是固定效应模型(fixed effect model),另一种是随机效应模型(random effect model)。
假定纳入Meta分析的各个独立研究来自一个相同的总体,研究间的差别只是抽样引起,各个独立研究的效应是效应合并值这一总体参数的估计值,效应合并时只考虑研究内变异。这种情况下,就应该选择固定效应模型。
假定纳入Meta分析的各个独立研究来自不同、但互有关联的一些总体,每个研究有其相应的总体参数,研究间的差别不仅仅是抽样引起,效应合并时不但考虑各研究内的变异,还考虑研究间的变异。这种情况下,就应该选择随机效应模型。
随机效应模型比固定效应模型"保守",即有更宽的95%置信区间(95%CI)和较少的机会出现"统计学的显著性差异"。随机效应模型不能解释研究间的异质性,也不能矫正偏倚或控制混杂。
研究间同质性较好,可以选用固定效应模型;研究间有异质性,则选用随机效应模型,或做其他处理后再做Meta分析。
如果各个研究间结果不存在异质性(P>0.10),选用固定效应模型,定量资料一般采用inverse-variance法(倒方差加权法);定性资料一般采用Mantel-Haenszel法(简称M-H法或Peto法)。
如果存在异质性,但合并资料仍然具有临床上的意义,可采用随机效应模型Dersimonian-Laird法(简称D-L法)。
二者区别在于计算合并效应量时权重不同,随机效应模型D-L法增大了小样本资料的权重,减小了大样本资料的权重,应用时对结论的解释要全面考虑。
无论采用何种模型得到的合并统计量,均需要通过假设检验的方法来推断合并后的综合效应量有无统计学意义。
Meta分析中效应量结果常用森林图(forest plot)来表示。森林图中的垂直线代表无效应线,水平线代表每个研究的结果,水平线中间的方块代表研究结果的点估计值,方块大小代表该研究在Meta分析中的权重,线宽代表研究结果的95%CI。如果该可信区间穿过垂直线,表示此95%CI包括无效线,文献结果为两对比组间差异无统计学意义;如果该可信区间在无效线右侧或左侧,表示此95%CI不包括无效线,文献结果为两对比组间差异有统计学意义。右侧为试验组的效应量大于对照组,左侧表示试验组的效应量小于对照组。森林图中的菱形块代表Meta分析合并后效应量估计值及95%CI。见图1。
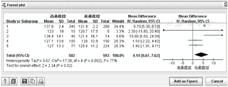

敏感性分析(Sensitivity Analysis)用于评价Meta分析结果是否稳定和可靠,发现影响Meta分析结果的主要因素,发现产生不同结论的原因。敏感性分析只有纳入可能低质量文献时才有必要做。常用的敏感性分析方法有:(1)按不同的研究特征,对纳入的文献进行分层Meta分析,考察结论有无变化;(2)采用不同模型(固定效应模型或随机效应模型)计算效应合并值的点估计和区间估计,考察结论有无变化;(3)从纳入研究中剔除质量相对较差的文献后重新进行Meta分析,考察结论有无变化;(4)改变研究的纳入和剔除标准(如是否包括未发表的研究等)后,对纳入的研究重新进行Meta分析,考察结论有无变化。无变化表示结果稳定,反之,结果稳定性差。
发表偏倚是指"统计学上有意义"的阳性研究结果较"统计学上无意义"的阴性研究结果或无效的(null)的研究结果更容易被发表。发表偏倚的产生有三个来源,分别为作者、研究的赞助者和杂志社的编辑。发表偏倚对Meta分析结果的真实性和可靠性有很大的影响,特别是当入选Meta分析的研究主要是以小样本研究为主时。发表偏倚常使Meta分析的效应合并值被高估,甚至使结论逆转,产生误导。
发表偏倚可采用漏斗图(funnel plots,funnel graphs)来进行识别,见图2。漏斗图是以效应大小为横坐标,样本量为纵坐标作的散点图。如果没有发表偏倚,理论上纳入Meta分析的各个独立研究效应的点估计在坐标轴上的集合应该呈一倒置的漏斗形。漏斗图上的点是围绕研究效应点估计的真实值对称地散开的,且小样本研究的效应散开在漏斗图的底部,随着样本含量增加,散点趋向密集,大样本研究效应的点估计密集在一个较窄的范围内。如果漏斗图不对称或不完整则提示可能存在发表偏倚(通常包含了阴性的研究结果)。


Meta分析的总结报告可以参考近年来国际上提出的随机对照试验(the quality of reporting of Meta-analysis of randomized controlled trials,QUOROM)和观察性研究(Meta-analysis of observational studies in epidemiology,MOOSE)的Meta分析声明进行总结报告撰写。
为评价噪声暴露程度对收缩压(SBP)的影响,现按事先确定的纳入和剔除标准筛选了5篇符合要求的独立研究文献资料,见表3。试作Meta分析。

5个噪声暴露程度对收缩压影响的研究结果
5个噪声暴露程度对收缩压影响的研究结果
| 研究 | 高暴露组 | 低暴露组 | ||||
|---|---|---|---|---|---|---|
| nli | 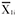 | S1i | n2i | 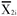 | S2i | |
| 1 | 345 | 137.6 | 2.4 | 200 | 131.9 | 2.2 |
| 2 | 15 | 123 | 19 | 5 | 120.7 | 17.5 |
| 3 | 40 | 136.4 | 14.1 | 14 | 121.4 | 16.1 |
【分析】 本资料为定量资料,血压的测量方法和度量衡相同,因此选用WMD作为效应指标。
【操作】 (1)创建一个新的系统评价:打开"New Review Wizard"对话框,按向导进行,其中"Type of review",选择"Intervention review",研究的Title中的"Intervention"为"噪声暴露程度","Health Problem"为"收缩压","Stage"对话框中选择"Full review"。(2)录入纳入文献信息:点开大纲页面的"Studies and references"下面的"Reference to studies",将光标指向"Included studies",单击鼠标右键选择"Add Study"(或在内容页面"Included studies"下面点击"Add Study",打开一个"New Study Wizard"窗口,录入研究的ID,如"Joan 2010"(一般为第一作者姓名和文献发表年),点击"Next",根据下拉菜单选择数据来源"Data source",点击"Next",录入研究年代,如"2010",单击"Next",新弹出的对话框询问是否有其他识别号,如果有就添加;否则进入下一步。点击"Next",选择"Add another study in the same section",点击"Finish"。重复以上步骤可以添加其他纳入文献信息。录入最后一篇纳入文献后,选择"Nothing",点击"Finish",此时在大纲页面双击"Included studies"即可显示出已添加的文献清单。(3)添加比较组:在大纲页面将光标指向"Data and analyses"单击鼠标右键选择"Add Comparison",打开窗口"New Comparison Wizard",在"Name"处输入比较的名称,如本例为"高暴露组与低暴露组",点击"Finish"。(4)添加数据类型:在大纲页面双击"Data and analyses",将光标指向上一步添加的比较组,如本例为"高暴露组与低暴露组",单击鼠标右键选择"Add outcome",或在内容页面"高暴露组与低暴露组"下面点击"Add outcome",打开一个"New outcome Wizard"窗口ꎬ选择"Data Type",本例为定量资料,所以选择"Continuous",点击"Next",输入变量名"Name"与组别标签"Group Label",本例为"收缩压"和"高暴露组"、"低暴露组",点击"Next",选择使用的统计分析方法,本例选择"Inverse Variance",分析模型为"Random Effects"。效应测量为"Mean Difference",点击"Next",直至选择"Add study data for the new outcome"。点击"Finish"。(5)录入数据:进入"New Study Data Wizard",按住Control键不放,选中前面录入的纳入文献,点击"Finish"(图3)。此时在内容页面打开数据录入表(图4),在此表格中输入每个纳入研究中两组的均数Mean、标准差SD以及样本含量Total。
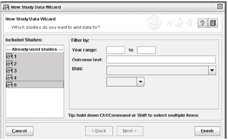



【结果】 RevMan会自动计算并显示结果如下(图5)。
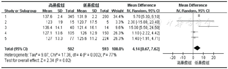

【解释】 结果中有每个研究以及所有研究合并的效应指标(本例为"Mean Difference")和"95%CI",结果以森林图显示,森林图屏幕底部有一个滑动标尺,拖动滑块可以改变标尺范围,可使森林图更加美观,在结果中还显示了每个研究的权重比重(%)、异质性检验结果(固定效应模型为CHI2与Ⅰ2,随机效应模型为Tau2、CHI2与Ⅰ2)和合并效应的假设检验结果。本例异质性检验χ2=17.36,P=0.002,Ⅰ2=77%,可以认为纳入研究的5篇文献存在异质性,所以选用随机效应模型,τ2=9.07,合并效应量为4.14,其假设检验:Z=17.36,P=0.02,合并效应量的95%CI为(0.67,7.62),说明通过此Meta分析可以认为噪声暴露不同程度对收缩压有影响,高暴露可以升高收缩压。
为了研究阿司匹林对心血管事件发生的预防作用,搜集了满足要求的7项临床随机对照试验,研究结果见表4,试进行Meta分析。
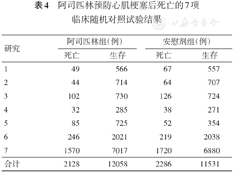
阿司匹林预防心肌梗塞后死亡的7项临床随机对照试验结果
阿司匹林预防心肌梗塞后死亡的7项临床随机对照试验结果
| 研究 | 阿司匹林组(例) | 安慰剂组(例) | ||
|---|---|---|---|---|
| 死亡 | 生存 | 死亡 | 生存 | |
| 1 | 49 | 566 | 67 | 557 |
| 2 | 44 | 714 | 64 | 707 |
| 3 | 102 | 730 | 126 | 724 |
| 4 | 32 | 285 | 38 | 271 |
| 5 | 85 | 725 | 52 | 354 |
| 6 | 246 | 2021 | 219 | 2038 |
| 7 | 1570 | 7017 | 1720 | 6880 |
| 合计 | 2128 | 12058 | 2286 | 11531 |
【分析】 本资料为定性资料,研究阿司匹林对心肌梗塞后死亡发生的预防作用,因此选用OR值作为效应指标。
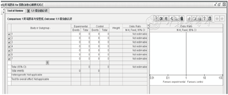
【操作】 (1)创建一个新的系统评价,Title中"Intervention"为"阿司匹林","Health problem"为"预防心肌梗塞死亡"。(2)仿上例录入纳入文献信息。(3)添加比较组,比较的名称为"阿司匹林与安慰剂"。(4)添加数据类型ꎬ"Data Type"为"Dichotomous",变量名"Name"为"死亡",组别标签"Group Lable"为"阿司匹林"、"安慰剂",选择使用的统计分析方法为"Peto",分析模型为"Fixed Effect",效应测量为"Odds Ratio"。(5)录入数据,仿上例在数据录入表(图6)中输入数据。

【结果】 计算结果如下(图7)。


【解释】 本例异质性检验 χ2=9.97,P=0.13,Ⅰ2=40%,可以认为纳入研究的7篇文献具有同质性,所以选用固定效应模型,合并效应量OR=0.90,其假设检验:Z=3.29,P=0.001,合并效应量的95%CI为(0.84,0.96),说明通过此Meta分析可以认为阿司匹林对心肌梗塞后死亡有预防作用。
【引申】 注意在森林图的上方有一工具条如图8,可以添加研究、改变效应指标、改变模型、显示森林图、显示漏斗图、计算器,还可以通过点击特性按钮( Properties)来对效应指标、模型等进行编辑和修改。


所有作者均声明不存在利益冲突


























