
本研究对2021—2025年北京市昌平区结核病报告发病率进行预测,为未来当地结核病防治工作的开展提供一定参考。
利用2010—2020年北京市昌平区结核病报告发病数据和常住人口数计算各年报告发病率;通过时间序列分析、回归模型、灰色模型对2010—2018年数据进行拟合,通过2019—2020年数据进行外部验证;最终拟合全部数据对2021—2025年报告发病率进行预测。
3种模型拟合效果均较好,残差均不超过1%。3种模型预测结果均显示,预计到2025年,结核病报告发病率较2015年下降约28.87%~31.21%。
3种模型均适用于拟合昌平区结核病报告发病数据,且预计2021—2025年昌平区结核病报告发病情况呈现下降趋势。

本刊版权归人民卫生出版社有限公司所有。任何机构或个人欲转发本刊图文,请与本刊联系。凡未经授权而转载、摘编本刊文章者,本刊将保留追究其法律责任的权利。
结核病仍然是严重威胁人类健康的全球性公共卫生问题[1]。2014年世界卫生组织制定了宏伟的"终止结核病策略",其目标旨在:与2015年相比,①到2035年结核病死亡人数下降95%;②结核病发病率下降90%(发病率低于10/10万);③没有因结核病而导致的家庭灾难性支出[2]。尽管全世界在结核病防治上已经取得了一定进步,但是距离2035年的目标还相差甚远[3]。为了达到这一目标,每个国家、每个地区都应该做出自己的努力,实现本地的目标。因此,为了评价当地结核病的流行状况、总结目前防治措施的实施情况,有必要定期对当地结核病疫情进行评估与预测,以便为更好地开展后续工作提供参考。本研究利用2010—2020年北京市昌平区结核病报告发病数据对未来5年当地的结核病疫情做出预测,以期为未来北京市昌平区结核病防治工作的开展提供一定参考。
北京市昌平区结核病发病数据来源于"结核病信息管理系统"中传染病报告卡的个案信息。按照发病日期在2010年1月至2020年12月、现住址为北京市昌平区进行筛选、统计,获得结核病发病数据。研究所涉及的2010—2020年北京市昌平区常住人口数据来源于《中国疾病预防控制信息系统》的《基本信息系统》。通过结核病报告发病数据和常住人口数计算当年的结核病报告发病率。本研究向北京市昌平区结核防治所伦理委员会申请免除知情同意并获批通过。
时间序列分析中的自回归滑动平均模型(ARIMA)是一种重要的预测模型。数据平稳化后,通过自相关系数(ACF)和偏相关系数(PACF)的性质确定p阶自回归系数和q阶移动平均系数[4]。对残差自相关进行统计学检验以确定是否为白噪声。通过AIC原则确定最优模型并进行预测[5]。
通过散点图判断报告发病率随时间的变化情况(线性模型、对数线性模型、指数模型),然后采用对应模型拟合数据并预测[6]。
以2010—2018年昌平区结核病报告发病率数据拟合上述3种模型并对2019—2020年报告发病率进行预测。将2019—2020年预测结果与实际结果进行比较,判定预测效果。最后充分利用2010—2020年数据通过拟合3种模型对2021—2025年昌平区结核病报告发病率进行预测。
所有数据整理、数据分析通过SAS 9.4完成。在统计检验过程中,检验水平α=0.05。
2010—2020年昌平区共报告结核病病例8 930例,结核病报告发病率呈现逐年下降趋势(t=-19.10,P<0.01),年平均递降率为3%(表1)。
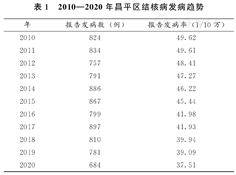
2010—2020年昌平区结核病发病趋势
2010—2020年昌平区结核病发病趋势
| 年 | 报告发病数(例) | 报告发病率(1/10万) |
|---|---|---|
| 2010 | 824 | 49.62 |
| 2011 | 834 | 49.61 |
| 2012 | 757 | 48.41 |
| 2013 | 791 | 47.27 |
| 2014 | 886 | 46.22 |
| 2015 | 867 | 45.44 |
| 2016 | 799 | 41.98 |
| 2017 | 897 | 41.93 |
| 2018 | 810 | 39.94 |
| 2019 | 781 | 39.09 |
| 2020 | 684 | 37.51 |
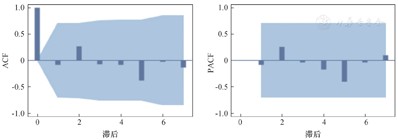
对2010—2018年报告发病率数据进行1阶差分后可以使序列平稳,ADF单位根检验结果显示Dickey-Fuller Tau=-5.45(P=0.01)。通过试凑并观察ACF和PACF的截尾和拖尾情况,判断p=1、q=1(图1)。此时AIC最小,为25.14,模型检验残差自相关检查统计量χ2=4.86(P=0.43),证明为白噪声序列。

根据2010—2018年数据对2019—2020年昌平区结核病报告发病情况进行预测显示,预测值与实际观测值之间残差不超过1%,且实际观测值在预测值95%CI内,说明ARIMA(1,1)可以较好地对数据进行拟合与预测。采用ARIMA(1,1)拟合2010—2020年整体数据对2021—2025年结核病报告发病情况进行预测显示,报告发病率仍然呈现下降趋势(表2,图2)。到2025年结核病报告发病率较2015年下降约30.79%。
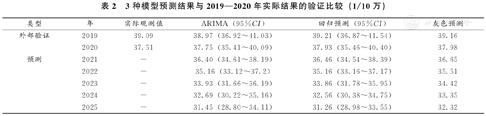
3种模型预测结果与2019—2020年实际结果的验证比较(1/10万)
3种模型预测结果与2019—2020年实际结果的验证比较(1/10万)
| 类型 | 年 | 实际观测值 | ARIMA(95%CI) | 回归预测(95%CI) | 灰色预测 |
|---|---|---|---|---|---|
| 外部验证 | 2019 | 39.09 | 38.97(36.92~41.03) | 39.21(36.87~41.54) | 39.16 |
| 2020 | 37.51 | 37.75(35.41~40.09) | 37.93(35.46~40.40) | 37.98 | |
| 预测 | 2021 | - | 36.40(34.61~38.19) | 36.46(34.54~38.39) | 36.65 |
| 2022 | - | 35.16(33.12~37.2) | 35.16(33.16~37.17) | 35.51 | |
| 2023 | - | 33.93(31.66~36.19) | 33.86(31.78~35.95) | 34.42 | |
| 2024 | - | 32.69(30.22~35.16) | 32.56(30.38~34.75) | 33.35 | |
| 2025 | - | 31.45(28.80~34.11) | 31.26(28.98~33.55) | 32.32 |
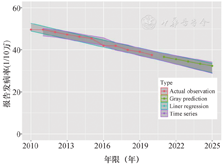

通过散点图可以看出,2010—2020年间,昌平区结核病报告发病率呈现线性下降趋势(t=-19.10,P<0.01)(图2)。因此利用2010—2018年的报告发病率与年份拟合线性回归方程(R2=0.96,β=-1.28,t=-12.37,P<0.01)。根据上述拟合方程对2019—2020年报告发病率进行预测,预测值与实际观测值之间残差不超过1%,且实际观测值在预测值95%CI内,说明线性模型也可以较好地对数据进行拟合与预测。采用线性回归模型拟合2010—2020年整体数据对2021—2025年结核病报告发病情况进行预测显示,报告发病率仍然呈现下降趋势(表2,图2)。到2025年结核病报告发病率较2015年下降约31.21%。
通过事前检验得知所有数据适合进行GM(1,1)模型。经过拟合优度检验,后验差C值为0.13(<0.35),均方差比值为一级,模型预测精度等级合格,可以用于外推预测。根据2010—2018年数据对2019—2020年数据进行预测,预测值与实际观测值之间残差不超过1%,说明灰色模型也可以较好地对数据进行拟合与预测。采用灰色模型拟合2010—2020年整体数据对2021—2025年结核病报告发病情况进行预测显示,报告发病率仍然呈现下降趋势(表2,图2)。并且灰色模型预测值均在时间序列分析和回归模型分析预测值的95%CI范围内。到2025年结核病报告发病率较2015年下降约28.87%。
及时对某一地区的传染病疫情流行状况进行分析、评估、预测,是掌握传染病流行规律、评价防控措施效果的重要内容[9]。而众多预测模型是评价传染病疫情趋势很好的工具[10]。ARIMA、回归模型、灰色模型都是短期预测疾病流行趋势的定量预测方法[11]。ARIMA是时间序列分析预测方法中较常用的一种模型,该模型充分考虑了事物自身发展的延续性和周期性,从理论上更加符合疾病发展的规律,更加适合传染病流行规律的预测;线性回归模型是经典的预测模型,在符合某种特定分布的情况下,可以很好地反应自变量与因变量之间的关系,但其缺点是不能对长期趋势进行预测;灰色系统理论是把一般系统论、信息论及控制论的观点和方法同数学方法结合起来,发展出的一套解决信息不完全系统的理论和方法,其中GM(1,1)是应用最为广泛的预测模型,其缺点是缺乏疾病的内在理论基础[5,12,13]。但上述3种方法在结核病疫情预测中均有许多应用[6,14,15]。本研究与既往研究的不同之处在于,通过3种预测方法对昌平区结核病报告发病率情况进行预测与评估。外部验证结果提示3种模型的预测结果均较好(残差不超过1%),能够进行适当外推预测。因此,本研究在拟合全部数据基础上,对未来5年的结核病报告发病情况进行预测。预测结果提示,未来5年昌平区结核病报告发病均呈平稳下降趋势。3种模型方法原理不同,但是预测结果相同,结论更加可靠。
既往研究利用2009—2014年的昌平区结核病报告发病数据,通过ARIMA对2015年的结核病发病数进行预测[16]。该研究仅对1年的报告发病绝对数进行了预测,而并未对未来的结核病流行趋势进行预测。本研究在3种预测模型基础上,对未来5年的结核病报告发病情况进行预测。结果提示:虽然整体结核病报告发病情况呈现持续下降趋势,但是到2025年报告发病率较2015年仅下降了28%~31%,距离世界卫生组织"终止结核病策略"的目标仍有较大差距。特别是目前距离起始点2015年还比较近,下降幅度相对较大。随着时间的推移,结核病疫情不断下降,则每年的疫情下降幅度会越来越小,达到"终止结核病策略"目标的压力也会越来越大。因此若想进一步加快降低昌平区结核病的疫情,在现有条件下,除了加大对患者发现和治疗管理的力度以外,还应实施社会、环境和经济干预,才有可能达到终止结核病的目标[17]。
本研究的局限性:①与其他疾病流行的模型预测研究一样,结核病的发生发展报告受社会、环境、个体因素等多种因素影响。如果收集更多影响结核病报告发病的因素并纳入模型分析,在更高维度上拟合数据,可以为更为精确的评估及预测疾病流行提供更多思路。②由于灰色模型的特点,只能进行单点预测,不能计算可信区间。
综上所述,任何模型预测方法都存在优点和缺点。但是只要根据数据特点采用适合的分析方法对疾病流行进行预测,就可以帮助疾病预防控制人员了解疾病的流行规律、掌握后续的发展趋势,为制订更为合理的防治措施提供依据。因此,本研究采用的3种模型对昌平区结核病报告发病情况进行预测,结果均提示未来5年结核病报告发病情况呈现平稳下降趋势,且残差比例小,数据拟合较好,预测结果可靠。



























