
探索循环呼吸条件下人体上呼吸道内压力分布和变动情况。
基于CT扫描图像建立口腔-二级支气管模型,仿真研究呼吸流量为60 L/min条件下,循环呼吸过程中模型各部位的压力变化及最大瞬时吸气或呼气时刻的压力分布。
呼吸流量增大时,上呼吸道腔体内压力差也随之增大;在咽部、喉部、气管分岔处这些具有特殊结构的部位呈现压力梯度的变化,集中在会厌下缘至气管处及气管分岔处。
呼吸道解剖结构形态与气流运动相应的力的分布和变化,交互作用并共同影响呼吸过程。压力循环变动的流场特性可为探讨气溶胶沉积以及一些呼吸道疾病的发生和治疗提供依据。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
呼吸系统疾病常见且多发。流行病学调查证实其与空气污染、吸烟、人口老龄化等因素密切相关。尤其是近年来,我国空气污染日益严重,各种吸入性变应原的种类及数量增多,导致呼吸系统疾病死亡率逐年上升,严重危害着人类的健康。呼吸系统承担机体和外界气体的交换活动,由呼吸道和肺组成。呼吸道以环状软骨为界分为上下两部分,喉以上为上呼吸道,气管和支气管为下呼吸道。人体各种系统中呼吸系统与外环境接触最频繁,其中上呼吸道是人体呼吸系统的门户。
呼吸过程中,人体通过吸入O2排出CO2完成气体的吐故纳新,其动力是肺内和大气之间的压力差。受呼吸道结构特征、分泌物、壁面弹性以及呼吸流量、空气中颗粒物等多种因素的影响,人体上呼吸道内的压力会时刻发生变化。压力变动是人体上呼吸道和气管内气流运动的显著特点,由此形成的压力梯度直接影响气溶胶颗粒在人体上呼吸道、主气管及各级支气管的运动轨迹、滞留时间以及沉积模式。研究人体上呼吸道内与气流运动状况相对应的压力循环变动形式,有助于准确理解人体上呼吸道的气溶胶颗粒的沉积规律,对辅助评价环境污染颗粒物、病毒气溶胶和药物气溶胶的剂量—健康效应也极具价值。
国内外学者在呼吸道内的流场特性和颗粒物沉积方面开展了大量有意义的工作,多集中在呼吸道内气流速度和分布[1,2,3,4]、压力和剪应力分布[5,6]、气溶胶沉积状况和规律[7,8]等方面。研究方法包括实验和数值仿真,实验又分为离体实验和活体实验。Corcoran等[9]采用荧光染料和激光多普勒方法,基于尸源性模型开展离体实验,测量上呼吸道内压力对呼气气流作用以及对颗粒沉积的影响研究。离体实验中组织器官无法保持原貌,结果的准确性受限是其问题所在;活体实验通常局限于猪,狗,大鼠等实验动物,由于它们的上呼吸道结构与人体差异较大,导致研究结果的说服力有限[10]。基于医学影像技术的长足发展和进步,近年来获取上呼吸道扫描数据和图像建立仿真模型,研究其流场特性的数值仿真方法日益受到青睐,具有无创伤、重复性高、周期短等优势。在压力研究方面,Ma等[11]通过建立人体上呼吸道到肺的数值模型进行仿真研究,发现呼吸频率对人体上呼吸道内阻力与肺部总阻力的比值的影响,0~1 Hz时比值为45%~70%,1~8 Hz时比值为70%~81%。Grotberg等[12]仿真研究发现人体呼吸管内呼吸流的黏性流体流动现象;Yang等[13]进一步研究了肺动脉交叉处的流体结构相互作用,发现透壁压力低于一定阈值时将引起可收缩管的收缩,压力随之迅速增大出现压降极限,引发自激振动等现象。孙秀珍等[14]通过研究建立的鼻-气管模型,发现在吸气最大时刻整个腔体中气压最高值位于前鼻孔处,最低值出现在喉咽和喉前庭附近;呼气最大时刻气压恰好与此相反。
据已有报道,针对上呼吸道内压力的绝大多数研究其关注重点均在压力分布方面,而缺乏对呼吸道解剖结构形态和与气流运动状况相对应的力学性能及其交互关系的研究和分析。基于此,本研究旨在研究人体上呼吸道及前二级支气管内压力循环变动。通过对健康国人的CT扫描图像进行处理、建模,构建数值仿真模型,利用大涡模拟方法[15],对呼吸流量为60 L/min的中等运动状态下的人体上呼吸道精细流场进行模拟研究,以期揭示呼吸过程中不同阶段呼吸道不同部位与气流运动相对应的压力循环变动的流场特性及其交互关系。
上呼吸道结构与其流场特性密切相关。建立基于真实人体的上呼吸道模型,对于定量分析上呼吸道结构与流场特性的交互关系至关重要。目前常见的人体上呼吸道气流运动研究主要基于口腔至气管的简化模型[16,17,18]。本研究首先对原始CT扫描数据进行预处理,再利用软件UG建模,最后进行规范化处理,建立了上呼吸道模型,包括口腔-咽-喉-气管-前二级气管(图1)。比以往报道的简化模型更为细致准确,尤其是咽、喉、气管分岔这些部位,支气管为非对称式的结构。除壁面弹性和软骨结构之外,本模型非常接近于真实人体上呼吸道,以此进行数值模拟更具实际意义。


质量守恒、动量守恒和能量守恒是最基本的物理守恒定律,流体流动同样遵守这些基本定律,如果是湍流流动,系统还要遵守湍流输运方程。根据这几个守恒定律,即可对流体运动的控制方程(governing equation)进行推导并进行数学描述。
大涡模拟是目前流体数值仿真研究最为热门的数值仿真方法之一。将N-S方程进行滤波处理后即可得到大涡模拟的基本控制方程,其张量形式[15]为
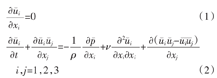
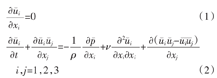
式中: 为流体速度大尺度分量,
为流体速度大尺度分量, 为流体压力大尺度分量,ρ为流体介质密度,ν为流体运动黏度。式(2)存在不封闭项(
为流体压力大尺度分量,ρ为流体介质密度,ν为流体运动黏度。式(2)存在不封闭项( ),定义为亚格子应力τij,为
),定义为亚格子应力τij,为


亚格子应力可见于小尺度脉动和可解尺度湍流之间,可经滤波过滤的动量输运,因而须建立封闭的亚格子应力方程才能实现大涡模拟。本研究采用Smagorin sky模式,则


式中:δij为Kronecker记号,νT为亚格子涡黏性系数, 为应变率张量,νT和
为应变率张量,νT和 定义如下
定义如下


式中: ,Cs为Smagorin sky常数,通常取数值为0.1~0.2,本研究计算中取0.1。
,Cs为Smagorin sky常数,通常取数值为0.1~0.2,本研究计算中取0.1。
网格划分把流体域划分成比较小而且互不重叠的子单元,是建立有限元模型的一个重要环节。网格的数量直接影响仿真计算结果的精度、计算时间以及对硬件设备的要求。一般情况下,计算精度随网格数量增加而提高,与此同时对计算时间和硬件设备要求也较高。优化的网格应有一定的自适应性,可细分模型上变化显著的区域而粗分变化平缓的区域,从而保证特殊结构位置的信息在不失真测量的情况下尽量减少计算量[19]。
网格划分影响实体的轮廓和光滑度,网格数量越多则实体表面越光滑,多面体面数越多则越接近平滑体。根据人体上呼吸道结构特征,为使其流场和边界层配合比较紧密,笔者将模型网格划分为两种类型,边界层划分为三棱柱网格以使该处得到最优的黏性处理,模型内部流场划分为四面体网格以节约计算机资源和缩短计算时间,并尽可能减小计算误差。
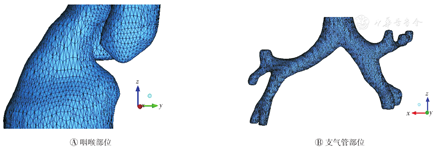
经过多次仿真实验筛选,本研究最后将模型划分成约1.5×106个网格,将三棱柱网格应用于近壁处,划分为细密的10层;其他区域采用四面体网格,最终满足了所需的精度要求。图2A、图2B分别是生成网格后的咽喉部和支气管部位。

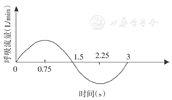
人的稳态呼吸通常有3种状态:休息状态、中等运动状态和剧烈运动状态,其所对应的呼吸流量分别为30、60、90 L/min。人们在日常生活中大多处于中等运动状态。为探索气流运动—压力循环变动交互关系,本研究仿真研究在呼吸流量为60 L/min的条件下进行。假定气流速度是时间的正弦函数,即瞬时呼吸流量呈正弦变化(图3)。由图可知,设定呼吸周期为3 s,吸气和呼气时间各为1.5 s,吸气和呼气阶段的呼吸气体量相等,约为1.5 L,则t=0.75 s和t=2.25 s分别是吸气和呼气流量最大的时刻。

本研究采用速度作为模型入口边界条件,假设呼吸入口气流速度稳定且在模型入口分布均匀;支气管出口处采用0相对压力的边界条件,其余量梯度为0。仿真计算在IBM M/T-M 6223-I2C服务器上实现,服务器具有3.0 GHz的CPU 2个,2.0 G内存。取Δt=0.000 5 s作为循环呼吸模式下的时间步长,采集每隔10步、共1~8 000步的流场计算过程数据集。
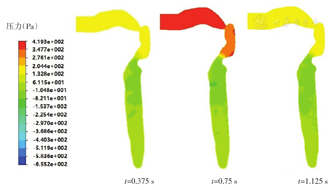
按60 L/min的循环呼吸条件,采用1.1节中建立的模型,采集呼吸过程中模型各部位的压力变化数据,包括吸气过程中吸气加速时刻t=0.375 s、瞬时吸气流量最大时刻t=0.75 s、吸气减速时刻t=1.125 s,吸气末呼气初的t=1.5 s时刻、瞬时呼气流量最大时刻t=2.25 s、呼气减速时刻t=2.625 s的压力变化信息。
由于口喉-主气管取的是正中矢状面而主气管-支气管取的是冠状面,因此分开显示吸气阶段不同时刻模型内的压力分布,其中口喉-主气管部分见图4,主气管-支气管部分见图5。口喉-主气管部分整个腔体最大和最小压力,在气流进入口腔后的t=0.375 s时刻分别约为170 Pa和-75 Pa,在t=0.75 s的吸气中间时刻分别约为419 Pa和-107.8 Pa,在吸气末的t=1.125 s时刻分别约为180 Pa和-65 Pa。可见,压力差值随着吸气流量变化而变化,吸气加速流量增大时其压力差也随之增大,吸气中间时刻瞬时呼吸流量最大时压力差值也到达峰值,然后又随吸气减速流量降低而减小,直到吸气终了与大气压基本保持平衡。瞬时吸气流量相近时刻t=0.375 s和t=1.125 s时,其压力差值相近。整个吸气过程中呼吸道压力最大值始终出现在口腔,最小值均位于声门后壁处。压力梯度变化集中在会厌下缘至气管处,在瞬时吸气流量最大时刻尤其明显。压力差从会厌-声门-气管先是逐渐减小而后又出现小幅增长,这是上呼吸道不同位置截面面积差异所致;此外,这些部位的前壁处的压力要高于后壁。

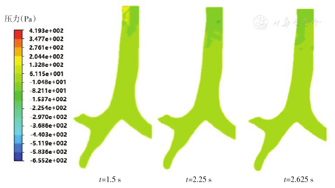

主气管-支气管冠状面压力分布仿真结果显示,压力总体分布较为均匀,梯度变化不如口腔-咽喉内明显。主支气管分岔处,t=0.375 s时压力约为15.20 Pa,无明显梯度变化;t=0.75 s时压力约为23.97 Pa,有微小的压力梯度;t=1.125 s时气压仅略高于大气压。此外,一级与二级支气管分岔处,压力较之于上级分岔小。(图5)
图6、图7分别是瞬时吸气流量最大时刻(t=0.75 s)口喉-主气管和主气管-支气管不同横切面的压力分布图。对比图6所示的截面A-A’至F-F’,可发现,从口腔到主气管压力逐渐减小,压力梯度变化极为明显。图6A显示口腔中压力分布较为均匀,压力呈上高下低,上部可达383 Pa,下部为378 Pa,较小的压力差致使压力梯度变化并不明显(图6B截面A-A’);咽部压力梯度明显,咽部左后和右后方压力较其他部位大,从后往前递减,约为145.1 Pa(图6B截面B-B’、C-C’);在喉部声门处,伴有半圆状压力梯度分布,压力最小值出现在声门左后方,约为-120 Pa(图6B截面D-D’);气流到达气管后压力分布均匀,仅个别点域有压力梯度(图6B截面E-E’、F-F’)。
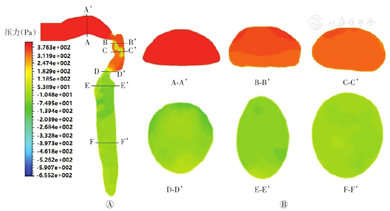

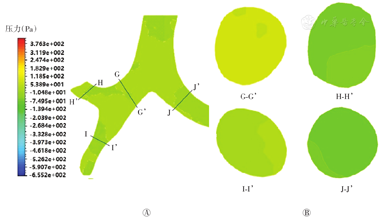

图7A显示,主气管-支气管冠状面整体压力分布均匀,从口腔到支气管递减。气流到达气管后,在靠近支气管的外壁有较小的压力梯度,分岔处压力最大,约为23 Pa;模型右侧靠上二级支气管内压力梯度较为明显(图7B截面H-H’、J-J’),靠近支气管分岔处的内壁处压力明显高于外壁的压力;支气管内其他区域也有不明显的压力梯度(图7B截面G-G’、I-I’),支气管内整体压力不大,约几帕至二十几帕。
图10为循环呼气过程中不同时刻口喉-主气管正中矢状面的压力分布图。可见在吸气末呼气初的t=1.5 s时刻,整个腔体压力分布均匀,为-3 Pa左右,基本接近标准大气压;在瞬间呼气流量最大的t=2.25 s时刻,上呼吸道内喉部声门和气管之间的压力梯度变化明显,从气管到口腔压力依次递减,气管内压力约为-28 Pa,口腔中约为-358 Pa,压力最小值出现在会厌部位靠近咽部前壁小区域,约为-655 Pa;在呼气减速的t=2.625 s时刻,各部位的压力有所上升,口腔中约为-160 Pa,气管内约为-14 Pa,压力梯度依然清晰可见。与循环呼气过程气流速度的正弦变化相适应,模型腔体内的压力差先是逐渐增大并取得峰值,之后逐渐回落至大气压水平,峰值约在瞬时呼吸流量最大时刻取得。
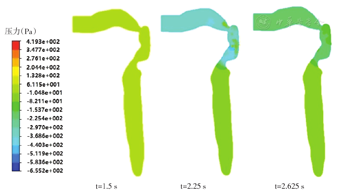

图11为主气管-支气管部分冠状面内压力分布图。可见在t=1.5 s时刻,管内压力为-1 Pa~-0.4 Pa,分布均匀且近似等于标准大气压;在t=2.25 s时刻,整体压力减小而压力差变大,压力梯度明显,在支气管分岔处压力梯度变化清晰可见,右侧一级支气管分岔处压力最大,约为-7 Pa;在t=2.625 s时刻,主支气管分岔处压力梯度变化明显,压力高于一、二级支气管分岔处压力。主气管-二级支气管的压力分布变化呈现出与气流速度流量相应的特点:吸气末呼气初压力分布均匀,随后压力差增大并于呼气流量最大的瞬时达到峰值;此外,随着气体途经各支气管向主气管会合,各级气管分岔处压力依次增大,至主支气管分岔处有明显压力梯度变化。呼气终了时刻,模型内压力基本与大气压保持平衡。
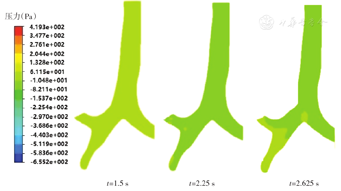

图12为瞬时呼气流量最大时刻口喉-主气管内不同截面的压力分布图。可见在呼气中间时刻,上呼吸道内压力梯度可见明显变化,并从气管到口腔压力呈递减趋势,整个口腔中压力分布均匀,压力在-357 Pa左右(图12A)。口腔中冠状面图12B截面A-A’所示,气流从咽部进入口腔,压力梯度不明显,但口腔中部压力低于外围压力,且上部压力大于下部,上部约为-355 Pa,而下部则为-370 Pa;图12B截面B-B’、C-C’所示,气流从喉部到达咽部,在咽部后壁主要是左后壁压力较其他部位大,而右前方有较小的压力梯度,压力最低值约为410 Pa;图12B截面D-D’所示,在喉部声门处,压力梯度变化也较为明显,压力最小值出现在声门右后方,约为-450 Pa;图12B截面E-E’、F-F’所示,气管内无明显压力梯度分布。
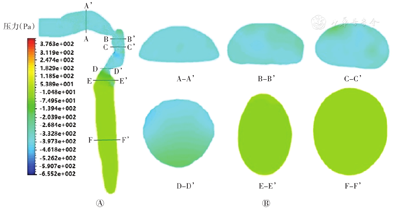

图13是同一时刻模型的主气管-支气管部分的不同截面的压力分布图。当气流从各级支气管会聚到上一级支气管并经主气管排出过程中,上述各部位压力分布整体均匀,靠近支气管分岔处的外壁有较小的压力梯度,压力最大位置仍处于分岔处,约为-7 Pa(图13A);图13B截面H-H’、J-J’内有较小的压力梯度,靠近支气管分岔处的内壁处压力明显高于外壁的压力;图13B截面G-G’、I-I’所示,支气管内其他区域无明显的压力梯度,循环呼气最大时刻整体压力从支气管到口腔呈递减趋势,压力差逐渐变大。
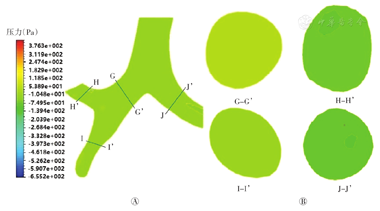

笔者研究的上呼吸道模型较以往的简化模型[16,17,18]在咽、喉、气管分岔和支气管这些部位更真实细致地反映了上呼吸道复杂的解剖结构,对探索结构形态与气流运动状况相对应的力学性能的交互关系有着更大的优越性。王莹等[20]基于Weibel模型建立的人体上呼吸道模型开展的数值仿真研究,指出正常人上呼吸道内的压力分布较为均匀,软腭至舌后根附近则有较为集中的梯度变化。本研究中,对结构复杂区域的压力分布进行了更为细致的仿真,验证了模型真实准确的必要性:吸气时压力最大、最小值分别出现在口腔和声门后壁处,呼气时分别出现在和会厌部位靠近咽部前壁,压力梯度变化集中在会厌下缘至气管处,口腔-咽喉内尤其明显。
与之前的稳态气流运动[16]和压力分布研究结果[21,22]相比,本研究基于CT扫描数据构建的数值仿真模型,提供了包括瞬时呼吸流量最大时刻在内的整个呼吸过程中,于不同时刻更加详细的与气流运动状况相对应的力学性能的数值模拟结果。相比Choi等[5]指出的呼吸气流流经上呼吸道内突起时产生较高压力和发生分离现象,结合胡桂林等[23]研究得出的咽部突缩几何结构导致气流速度剧烈上升和压力的急剧下降,内外压力差随呼吸强度增大而增大的结论,本研究通过仿真研究定量分析吸气和呼气过程中压力的分布的具体差异,并引入呼吸流量变化探索其对压力分布的影响。研究发现吸气过程中整个腔体最大最小压力值都出现在流量最大时候,在呼气流量最大时刻出现了最小压力值且该时刻会厌下缘至气管处和气管分岔处呈现出最为明显的压力梯度,为进行呼吸流量最大时刻压力分布分析提供了依据,进而进行了深入细致的分析。分析提示,除Choi等[5]指出的呼吸道内突起如咽、喉,呼吸道还有气管分岔和支气管这些位置,由于结构复杂,截面收缩或分岔,压力较大,气流速度变化剧烈,导致气溶胶易于沉积从而致病。此结论为流量最大时刻和疾病高发区也同样会是药物气溶胶易沉积的时刻和区域提供了依据。
笔者针对呼吸过程中人体上呼吸道的压力循环变动的数值仿真研究和分析,为人体上呼吸道气溶胶沉积规律预测和评估提供了仿真依据。未来进一步的研究应考虑人体上呼吸道气流运动中通常伴有涡结构特征以及气溶胶沉积受颗粒物尺寸、浓度、不同运动状态的呼吸流量等各多种因素影响,从而可从数值仿真研究向更为深入的实验研究方向发展。
无



























