
研究一种基于差分搜索的最大类间方差法,寻找多阈值对脑部磁共振图像进行有效分割。
通过BET(brain extraction tool)算法去除原始磁共振图像的非脑组织部分,使用BFC(best-fit with coalescing)算法去除强度不均匀性,使用差分搜索算法对图像进行最大类间方差寻优,找出最优阈值,从而对磁共振图像进行多阈值分割。使用BrainWeb提供的仿真磁共振脑部图像数据对方法进行验证。
对于不同噪声水平、强度不均匀性条件下的磁共振图像,所提出的基于差分搜索的最大类间方差法的分割效果均优于脑功能磁共振成像软件库(FSL)、统计参数图(SPM)和Brainsuite方法。
基于差分搜索的最大类间方差法有较好的分割精度与强健性,尤其对脑脊液有很好的分割效果。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
人脑是人体最复杂的组织器官,控制着学习、运动、交流等一系列行为。准确快速地对脑部组织结构进行图像分割,辅助医生诊断疾病,已成为目前医学界的一个热点研究方向[1]。磁共振成像(magnetic resonance imaging, MRI)是较为成熟、安全的成像技术,已广泛应用于脑部的临床检测[2]。MRI能实现多角度三维断层扫描成像,对大脑的脑白质(white matter, WM)、脑灰质(gray matter, GW)、脑脊液(cerebrospinal fluid, CSF)等成分均有较好的分辨率[3]。但脑部组织形态复杂,脑脊液、颅骨、头部空腔在MRI图像中的灰度值非常接近,且MRI图像可能受到噪声、偏移场(bias field, BF)引发的灰度不均匀性影响,使从MRI图像中准确分割各种组织变得十分困难[3]。为此,大量脑部MRI的自动分割方法被提出,如基于统计学、几何分布、解剖知识、深度学习等,并在此基础上开发了多种自动分割工具。例如,在神经成像分析中,广泛使用的软件包就具有头骨剥离、强度非均匀性校正、自动组织分割等功能。主流的图像分割软件包有统计参数图(statistical parametric mapping,SPM)[4]、脑功能磁共振成像软件库[functional MRI of the Brain(FMRIB)Software Library,FSL][5]、BrainSuite[6]。其中,SPM是由英国伦敦大学的威康信托基金会神经影像中心(Wellcome Department of Imaging Neuroscience)研发,其图像分割算法的核心是一种基于体素的形态学分析方法(voxel-based morphometry,VBM);FSL由英国牛津大学FMRIB分析小组编写,其FSL-FAST自动分割工具专为脑图像分割开发,算法核心是基于隐马尔可夫随机场(HMRF)模型,该模型使用期望最大化算法进行优化[7];BrainSuite由美国加利福利亚大学洛杉矶分校神经影像实验室和美国南加州大学生物医学成像研究小组共同研发,使用最大后验概率(maximum a posteriori, MAP)分类器进行分类[8]。上述工具为脑白质、灰质等重要脑组织的识别提供了便利,但总体来说,这些方法对于脑脊液的分割精度远低于脑白质和脑灰质,因为脑脊液的形态更为复杂且体积远小于脑白质和灰质。
阈值分割是一种传统的图像分割方法,广泛应用于医学图像分割,阈值的选择是其重点及难点[9]。最常见的多阈值分割方法是最大类间方差法,即大津法(OTSU),此外还有最大熵法、最小误差法、简单统计法等。脑部MR图像由于受噪声、强度不均匀性等因素的影响,普通的多阈值分割往往稳定性差且精度较低。但将脑部MR图像进行强度不均匀性自动校正,其得到的直方图能更好地区分出不同组织类别的灰度概率分布,表明可以基于OTSU进行多阈值分割。因此,本研究中采用去除强度不均匀性之后的脑组织(脑白质、灰质、脑脊液、背景)图像,将其类间方差作为目标函数,并采用稳定的寻优算法对多阈值进行寻优,使类间方差达到最大。
差分搜索(differential search,DS)算法是Civicioglu[10]于2012年提出的一种寻优算法。DS算法参考多个个体并选取最优值,能很好的权衡种群的探索和开发能力,具有全局收敛性和较快的收敛速度。Liu等[11]比较了DS算法与粒子群优化(PSO)算法、人工蜂群(ABC)算法、角度和时延联合估计(JADE)算法,群目标联合检测与估计(JDE)算法的优劣,结果表明DS算法更加快速、准确,且能较好地克服局部收敛,得到更高的搜索精度。因此,本研究中使用DS算法进行多阈值寻优。首先,将脑部MR图像进行强度不均匀性自动校正预处理,以便通过图像直方图更好地区分出不同组织类别的灰度概率分布;然后,计算预处理图像的OTSU,并使用DS算法对OTSU进行寻优,得到稳定的、准确率高的多阈值;最后,使用多阈值对原图像进行组织分割。结果表明,本研究采用的分割方法在偏移场和噪声并存的情况下,能得到较好的分类结果。
OTSU法是1979年由日本学者大津提出,是一种自适应确定阈值的方法,也称大津法[12]。脑组织分割中,最关注是脑白质、脑灰质和脑脊液。因此,在分割时首先需要将脑皮层去除,再对脑实质部分进行分割,得到脑白质、脑灰质、脑脊液及背景4部分。为此,需要3个阈值以便对脑实质图像进行分割。
假设一幅图像像素总数为N,灰度级为k,灰度值为q{q∈(0,k-1)}的像素数为nq。灰度值为q的概率为


用a,b,c{a,b,c∈(0,k-1)}3个阈值将图像分成N1=[1,a],N2=[a+1,b],N3=[b+1,c],N4=[c+1,k-1] 4个集合,则各集合的概率为
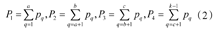
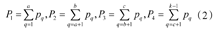
令g1、g2、g3、g4分别为集合N1、N2、N3、N4的平均灰度值。
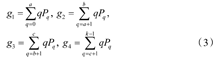
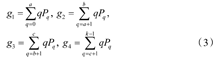
则全局灰度均值为


最大类间方差为
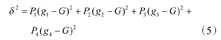
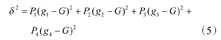
随着所选择的阈值a、b、c的不同,类间方差是变化的;当类间方差达到最大时,各类组织之间的区分度最好,阈值最优。更快地找到稳定的多阈值是下一步优化的任务。
DS算法是一种新型的仿生智能优化算法。其在求解优化问题过程中,假设种群是由人工生物超种群随机组成,生物种群将迁移到全局最优的位置。在首次迁移过程中,生物种群随机搜索,判断所发现的位置是否符合迁移条件,此时的位置称为栖息点;接着,从栖息点寻找下一个临时位置为停留点;直到找到最接近全局最小值的位置。
将Yi(i=1,2,…,L)记为生物种群中第i个搜索对象,L为表示生物种群的大小,yij(i=1,2,…,L;j=1,2,…,D)为第i个搜索对象的第j维取值,D表示优化问题的维度数,即搜索空间的维数。从而,由Yi生成超种群superorganismg(g=1,2,…,M),其中M为种群最大进化代数。DS算法在每一次迭代进化过程中,选择优势位置进行搜索个体的位置更新,保证了种群多样性,并且实现了群体向全局最优位置的运动,最终搜索到全局最优解[13],其算法主要步骤如下。
随机生成N个搜索个体,yij定义为
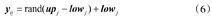
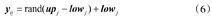
式中:lowj与upj分别表示搜索个体在j维的下限值和上限值。搜索种群为
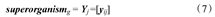
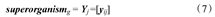
DS算法在进化中,按照下式进行种群搜索,在保证了种群多样性的条件下逐渐靠近最优解
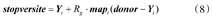
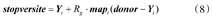
式中:Rg·mapi为搜索步长控制矢量,调节种群搜索位置变化的幅度;Rg·是由rand函数在(0,1)之间随机产生的随机数。mapi是0,1组成的随机向量。donor是每次进化前全部搜索个体随机排列的矩阵,从而通过(donor-Y)实现进化过程。stopversite是仿生变异后的结果,即是新生成的N个候选位置。
控制种群边界的目的是在搜索过程中,对维度超过边界范围的个体stopversitei重新赋值,确保搜索个体处于搜索范围中。即当stopversiteij<lowj或stopversiteij>upj时,按照下式赋值
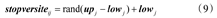
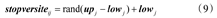
通过比较当前stopversitei与Yj的适应度值,若stopversitei优于Yj,则将Yj更新为stopversitei的位置,并记录最优解,完成一次迭代。当完成一定次数迭代,输出全局最优值。
脑皮层与颅骨会影响脑部MR图像的组织分割结果,因此首先需要对原始MR图像进行预处理。本研究中使用BET(Brain Extraction Tool 2.1)[14]工具包去除非脑组织(脑皮层与颅骨)。
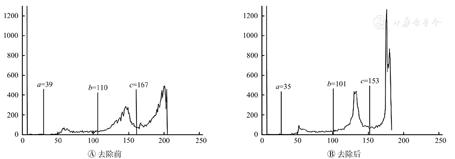
由于受脑部MR图像的强度不均匀性影响,直接使用OTSU多阈值分割结果不准确,因此使用BFC tool[7]去除强度不均匀性。图1A为图2B脑部图像对应的直方图,图1B为去除强度不均匀性后的直方图。可看出去除不均匀性后直方图的峰谷分布更为明显,更容易找到准确的最优阈值。图1的例子中,处理前的OTSU阈值为39、110和167,去除不均匀性后的OTSU阈值为35、101和153。


经过上述2个步骤的预处理之后,使用DS作为优化算法,最大类间方差(δ2)作为目标函数,对多阈值a、b和c进行优化(图3)。
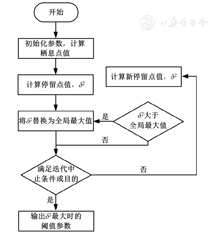

δ2—最大类间方差
为了定量地评价算法分割性能,采用戴斯相似性系数(Dice similarity coefficient,DSC)[15]对分割结果进行评价,如下式
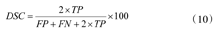
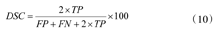
用S表示分割后目标区域像素点集合,T表示金标准目标区域像素点集合。式(10)中,TP为真阳性(true positive)数据集,TP=S∩T;FP为假阳性(false positive)数据集,FP=S-T;FN为假阴性(false negative)数据集,FN=T-S;DSC为评价结果,数值越接近100表示分割效果越好,DSC=100表示分割结果与金标准结果完全相同。
为了评估所提出分割方法的性能,选用BrainWeb仿真数据集[16]、MICCAI脑部病灶分割挑战赛真实数据[17]进行验证。BrainWeb是由加拿大McGill大学脑成像中心建立的仿真脑数据库,它提供了MR图像脑组织的标准分割结果,常被用来测试脑组织分割算法的有效性。本研究中,选取BrainWeb数据集中T1加权(图像尺寸181 pixels×217 pixels×181 pixels,层厚1 mm),分别加了0%、1%、3%和5%的噪声,射频强度不均匀性(radio frequency,RF)分别取0%、20%和40%。共生成12组模拟人脑MR图像为验证数据。MICCAI数据是波士顿儿童医院和北卡罗莱大学提供的真实脑部MRI图像(512 pixels × 512 pixels × 512 pixels,层厚1 mm)。
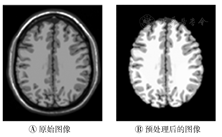
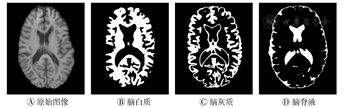
测试所用软件系统中,操作系统为Microsoft Windows 10,软件平台为MATLAB 2016B;硬件系统中,CPU为Intel Core i5 6400,内存为8 GB。为了验证分割算法的性能,首先使用BrainWeb脑部MR仿真数据集中T1加权图像进行实验。图2A为BrainWeb数据集中,处理前后的T1加权像的第100副断层图像,其噪声等级为0%,强度不均匀性为40%。分割后脑白质、灰质和脑脊液的DSC系数分别为99.12、96.14和90.16。
共对4种不同水平的噪声、3种不同偏移场下的12组图像进行了分割实验。不同RF和噪声等级下,FSL、SPM、Brainsuite和本方法对白质、灰质、脑脊液的分割效果对比,如图4所示。可看出在同等噪声水平下,随着RF的增加,本方法对白质、灰质和脑脊液的分割效能优于FSL、SPM和Brainsuite;而在相同RF条件下,随着噪声水平的增加,本方法对白质、灰质和脑脊液的分割效能同样优于FSL、SPM和Brainsuite。说明本方法具有较好的健壮性(robustness)。
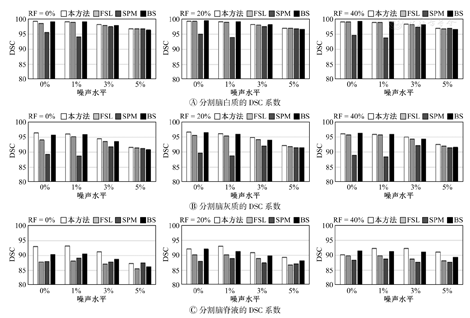

DSC—戴斯相似性系数;FSL—脑功能磁共振成像软件库;SPM—统计参数图;BS—BrainSuite;RF—射频不均匀性;本方法为基于差分搜索优化最大类间方差法
与FSL、SPM和Brainsuite方法比较,当噪声水平低、RF较强时,本方法所得DSC值最大,分割结果较准确;当噪声水平高、RF较弱时,噪声是影响分割结果的主要因素,而本文方法对噪声的健壮性更强,能获得更大的DSC值;当噪声和RF都很强时,所有方法的DSC值均下降,但本方法所得DSC值仍大于其他方法,分割效果也更好。
不同射频不均匀性条件下,各方法对0%、1%、3%和5% 4个噪声水平核磁图像分割的DSC均值结果,见表1。可见,本分割方法的MR图像分割效果最好,尤其对脑脊液的分割,其DSC系数相比其他方法高2%~3%。此外,又分别对T1加权图95~105副MR断层图像进行了分割实验,结果与第100副断层图像近似,本方法表现同样优于FSL、SPM和Brainsuite法。
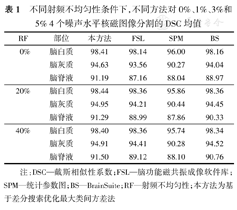
不同射频不均匀性条件下,不同方法对0%、1%、3%和5% 4个噪声水平核磁图像分割的DSC均值
不同射频不均匀性条件下,不同方法对0%、1%、3%和5% 4个噪声水平核磁图像分割的DSC均值
| RF | 部位 | 本方法 | FSL | SPM | BS |
|---|---|---|---|---|---|
| 0% | 脑白质 | 98.41 | 98.14 | 96.00 | 98.16 |
| 脑灰质 | 94.63 | 93.56 | 90.27 | 94.04 | |
| 脑脊液 | 91.19 | 87.16 | 88.04 | 88.97 | |
| 20% | 脑白质 | 98.44 | 98.36 | 95.86 | 98.36 |
| 脑灰质 | 94.95 | 94.21 | 90.44 | 94.45 | |
| 脑脊液 | 91.29 | 88.99 | 87.86 | 90.33 | |
| 40% | 脑白质 | 98.40 | 98.36 | 95.74 | 98.34 |
| 脑灰质 | 94.91 | 94.41 | 90.28 | 94.52 | |
| 脑脊液 | 91.50 | 89.12 | 88.10 | 90.76 |
注:DSC—戴斯相似性系数;FSL—脑功能磁共振成像软件库;SPM—统计参数图;BS—BrainSuite;RF—射频不均匀性;本方法为基于差分搜索优化最大类间方差法
本研究采用了MICCAI脑部病灶分割挑战赛真实数据中的T1加权图像进行分割,由于该数据集没有组织分割结果的金标准,虽不能定量的评价分割结果,但可以对不同方法进行横向比较。分割结果表明,基于DS优化最大类间方差分割法可较好地分割脑部真实图像数据(图5)。

由于组织强度不均匀性,噪声和部分体积效应等影响,从MR图像中分割脑组织中的白质、灰质和脑脊液是一项很有挑战的任务。本研究中使用基于DS优化最大类间方差的方法来对脑部组织图像进行分割,并使用了BrainWeb提供的仿真MR脑部图像数据进行了验证,考察了不同噪声水平、强度不均匀性条件下的MR图像分割效果。结果表明,该方法的分割准确率优于FSL、SPM和Brainsuite方法,尤其对脑脊液的分割效果更好。今后研究将结合图像位置信息进一步提升该方法的分割准确率。
所有作者均声明不存在利益冲突



























