胡佳; 田向阳; 陈继彬; 任学锋; 程玉兰

doi:10.3760/cma.j.issn.0254-6450.2019.02.021

点赞 0
分享 0
收藏 0
纠错

• 学习·发现·交流 •

中国居民传染病健康素养测评量表的结构方程模型分析

中华流行病学杂志, 2019,40(2) : 237-240. DOI: 10.3760/cma.j.issn.0254-6450.2019.02.021

摘要

目的

了解中国居民传染病健康素养测评量表不同维度之间的关系。

方法

采用结构方程模型，使用2015年3－5月在我国3个省份随机抽取的4 499名城乡居民传染病健康素养数据库，运用AMOS 21.0软件构建结构方程模型进行分析。

结果

结构方程模型适配度指标：适配度指数为0.969，调整后适配度指数为0.962，残差均方和平方根为0.038，渐进残差均方和平方根为0.038，标准化残差均方和平方根为0.032，非规准适配指数为0.926，比较适配指数为0.934，规准适配指数为0.925，相对适配指数为0.915，增量拟合指数为0.934，简约调整适配度指数为0.782，简约调整规准适配指数为0.817，简约调整比较适配指数为0.825，临界样本数为702，模型拟合效果良好。结构方程模型显示，传染病的基本知识与观念对传染病的预防、管理与治疗、辨认的总效应为0.771、0.744、0.843；传染病的辨认、预防对传染病管理与治疗的总效应分别为0.164、0.535。对传染病的管理与治疗影响强度最大的为传染病的基本知识与观念（55.4%）；其次为传染病的预防（28.6%）；而传染病的辨认影响较小（2.7%）。

结论

提高我国居民传染病健康素养，重点是改善个体的传染病基本知识与观念、传染病预防技能。

引用本文: 胡佳, 田向阳, 陈继彬, 等. 中国居民传染病健康素养测评量表的结构方程模型分析 [J] . 中华流行病学杂志, 2019, 40(2) : 237-240. DOI: 10.3760/cma.j.issn.0254-6450.2019.02.021.

参考文献导出: Endnote NoteExpress RefWorks NoteFirst 医学文献王

扫描看全文

正文

作者信息

基金 0 关键词 0

English Abstract

阅读 0 评论 0

相关资源

引用 | 论文 | 视频

版权归中华医学会所有。

未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。

除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。

中国居民传染病健康素养测评量表^[1,2]（infectious disease-specific health literacy，IDSHL）是由我国学者开发的用于测量居民传染病健康素养及评价传染病干预效果的工具。为了探讨IDSHL量表不同维度之间的关系，本研究基于课题组2015年3－5月调查我国中、东、西部3个省份城乡居民传染病健康素养的数据库，采用结构方程模型（Structural Equation Modeling，SEM），考评IDSHL量表SEM适配度，分析SEM潜变量之间的关系。

资料与方法

1．研究工具：

采用中国居民IDSHL量表^[1,2]，该量表第一部分包括22个条目（测量变量，依次标记为sa1~sa10，sb1~sb12），分属4个维度：F1：传染病的基本知识与观念（7个条目，主要考察个体对常见传染病的传染源、传播途径、易感人群等方面的基本知识与观念，如乙型肝炎可通过性行为传播）；F2：传染病的预防（7个条目，主要考察个体对常见传染病预防措施的了解情况，如小儿服用"糖丸"疫苗为了预防什么疾病）；F3：传染病的管理与治疗（4个条目，主要考察对常见传染病管理与治疗的掌握情况，如被病原体污染的水体管理）；F4：传染病的辨认（4个条目，主要考察个体对常见传染病病原体和症状的辨别能力，如肺结核症状）。4个维度的Cronbach’α分别为0.652、0.672、0.599、0.632，各条目的内容效度均≥0.8[该量表研制过程中邀请了10名在传染病防控、健康素养和健康教育方面具有20年以上工作经验的专家，按照专家小组意见集中法，对条目进行筛选，保留意见一致率≥80%的条目^[1]]，结构效度较好^[1,2]。IDSHL量表第二部分包括6个条目，属测量应答者认知能力的单独维度，不纳入分析。根据传染病健康素养的专业知识^{[1,2,3,4,5,6,7]}，F1设为外因潜变量（不受其他潜变量影响）；F2、F3、F4设为内因潜变量（受其他潜变量影响）^[8,9,10]。IDSHL量表4个潜变量之间相互影响的程度称为效应值，2个潜变量之间的直接影响称为直接效应，通过中间变量产生的影响称为间接效应，直接效应与间接效应的和称为总效应。

2．数据来源：

采用多阶段整群随机抽样方法，于2015年3－5月在我国浙江省嘉兴市、湖北省宜昌市和甘肃省兰州市收集的4 499名居民的传染病健康素养数据作为研究资料。其中男性2 167例（48.2%），女性2 332例（51.8%）；年龄（31.89±14.70）岁。本研究在拟合结构方程模型前，各层的主要变量均以得分进行了量纲统一化。

3．统计学分析：

采用AMOS 21.0软件构建SEM进行分析^[8,10]。模型评价指标包括正态性检验^[8,10]：偏度系数（skew）<3，峰度系数（kurtosis）<8。模型基本适配指标^[8,9,10,11]：模型误差项之间的协方差矩阵没有出现负数；参数估计值没有异常偏大的；参数估计值的t检验有统计学意义（t>1.96，P<0.05）；潜变量与其测量变量间的因子负荷量（λ）>0.4^[2,12]。整体模型适配指标^[8,10,13,14]：绝对适配统计量[χ²值、χ²/df、残差均方和平方根（RMR）、渐进残差均方和平方根（RMSEA）、标准化残差均方和平方根（SRMR）、适配度指数（GFI）、调整后适配度指数（AGFI）]、增值适配统计量[规准适配指数（NFI）、相对适配指数（RFI）、增量拟合指数（IFI）、非规准适配指数（TLI/NNFI）、比较适配指数（CFI）]、简约适配统计量[（简约调整适配度指数（PGFI）、简约调整规准适配指数（PNFI）、简约调整比较适配指数（PCFI）、临界样本数（CN）、Akaike讯息效标（AIC）、一致性Akaike讯息效标（CAIC）]。

结果

1．模型基本适配度：

数据分布正态性检验结果显示，22个测量变量的峰度系数绝对值介于0.239~1.999之间，<8；偏度系数绝对值介于0.033~1.819之间，<3；因此，采用最大似然法作为模型各参数估计方法。参数估计结果显示，各参数估计值的误差方差均没有负值，为0.037~0.148，t检验有统计学意义（P<0.05），见表1。22个测量变量的标准化参数估计值（λ）为0.160~0.731，其中18个λ>0.4，可见大部分λ在标准范围内，提示模型基本适配度良好，见图1。

点击查看表格

表1

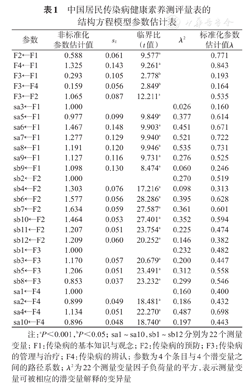
中国居民传染病健康素养测评量表的结构方程模型参数估计表

表1

中国居民传染病健康素养测评量表的结构方程模型参数估计表

参数	非标准化参数估计值		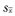临界比（t值）	λ²	标准化参数估计值λ
F2←F1	0.588	0.061	9.577^a		0.771
F4←F1	1.325	0.143	9.261^a		0.843
F3←F1	0.293	0.105	2.778^b		0.193
F3←F4	0.159	0.056	2.849^b		0.164
F3←F2	1.065	0.087	12.211^a		0.535
sa3←F1	1.000			0.026	0.160
sa5←F1	0.977	0.099	9.849^a	0.377	0.614
sa6←F1	1.467	0.148	9.903^a	0.451	0.671
sa7←F1	1.277	0.129	9.940^a	0.521	0.722
sa8←F1	1.191	0.120	9.946^a	0.535	0.731
sa9←F1	1.127	0.116	9.731^a	0.276	0.525
sb9←F1	1.098	0.130	8.474^a	0.060	0.246
sb2←F2	1.000			0.270	0.519
sb4←F2	1.303	0.076	17.216^a	0.098	0.313
sb6←F2	1.577	0.056	28.286^a	0.395	0.628
sb7←F2	1.634	0.059	27.587^a	0.361	0.601
sb10←F2	1.464	0.053	27.401^a	0.352	0.594
sb11←F2	1.207	0.051	23.754^a	0.225	0.474
sb12←F2	1.209	0.060	20.252^a	0.146	0.382
sb1←F3	1.000			0.232	0.482
sb3←F3	1.170	0.057	20.679^a	0.200	0.447
sb5←F3	1.206	0.051	23.491^a	0.312	0.558
sb8←F3	0.853	0.037	23.232^a	0.299	0.546
sa1←F4	1.000			0.160	0.400
sa2←F4	0.899	0.049	18.481^a	0.186	0.432
sa4←F4	1.134	0.051	22.270^a	0.487	0.698
sa10←F4	0.896	0.048	18.740^a	0.197	0.443

注：^aP<0.001，^bP<0.05；sa1~sa10，sb1~sb12分别为22个测量变量；F1：传染病的基本知识与观念；F2：传染病的预防；F3：传染病的管理与治疗；F4：传染病的辨认；参数为4个条目与4个潜变量之间的路径系数；λ²为22个测量变量因子负荷量的平方，表示测量变量可被相应的潜变量解释的变异量

点击查看大图

图1

中国居民传染病健康素养测评量表的结构方程模型

点击查看大图

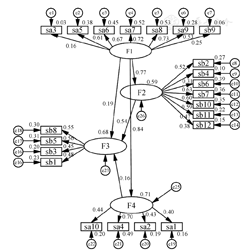
注：sa1~sa10，sb1~sb12分别代表22个测量变量；F1：传染病的基本知识与观念；F2：传染病的预防；F3：传染病的管理与治疗；F4：传染病的辨认

图1

中国居民传染病健康素养测评量表的结构方程模型

2．模型整体适配度：

整体模型配适度指标中，除χ²值（1 527.49）、χ²/df（7.488）和AIC（1 625.491）以外，其他统计量均达适配标准。见表2。

点击查看表格

表2

模型整体适配度检验表

表2

模型整体适配度检验表

统计检验量		适配标准或临界值	模型检验结果	模型适配判断
绝对适配统计量
	χ²值	P>0.05	1 527.490(P<0.05)	否
	χ²/df	<2（良好），<3（普通），<5（可以接受）	7.488	否
	RMR	<0.05	0.038	是
	RMSEA	<0.08（<0.05为优良；<0.08为良好）	0.038	是
	SRMR	<0.08（<0.05为优良；<0.08为良好）	0.032	是
	GFI	>0.9	0.969	是
	AGFI	>0.9	0.962	是
增值适配统计量
	NFI	>0.9	0.925	是
	RFI	>0.9	0.915	是
	IFI	>0.9	0.934	是
	TLI/NNFI	>0.9	0.926	是
	CFI	>0.9	0.934	是
简约适配统计量
	PGFI	>0.5	0.782	是
	PNFI	>0.5	0.817	是
	PCFI	>0.5	0.825	是
	CN	>200	702	是
	AIC	理论模型值<独立模型值，且同时<饱和模型值	1 625.491<20 421.393	否
		理论模型值<独立模型值，且同时<饱和模型值	1 625.491>506.000
	CAIC	理论模型值<独立模型值，且同时<饱和模型值	1 988.660<20 584.449	是
		理论模型值<独立模型值，且同时<饱和模型值	1 988.660<2 381.137

注：RMR：残差均方和平方根；RMSEA：渐进残差均方和平方根；SRMR：标准化残差均方和平方根；GFI：适配度指数；AGFI：调整后适配度指数；NFI：规准适配指数；RFI：相对适配指数；IFI：增量拟合指数；TLI/NNFI：非规准适配指数；CFI：比较适配指数；PGFI：简约调整适配度指数；PNFI：简约调整规准适配指数；PCFI：简约调整比较适配指数；CN：临界样本数；AIC：Akaike讯息效标；CAIC：一致性Akaike讯息效标

3．结构方程模型潜变量间关系：

传染病的基本知识与观念对传染病的预防、管理与治疗、辨认的总效应为0.771、0.744、0.843；传染病的辨认、预防对传染病管理与治疗的总效应分别为0.164、0.535。见表3。内因潜变量可以被外因潜变量解释的变异量为总效应值的平方（%），即对传染病的管理与治疗影响强度最大的为传染病的基本知识与观念（55.4%）；其次为传染病的预防（28.6%）；而传染病的辨认影响较小（2.7%）。

点击查看表格

表3

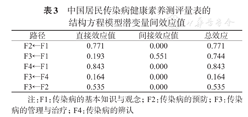
中国居民传染病健康素养测评量表的结构方程模型潜变量间效应值

表3

中国居民传染病健康素养测评量表的结构方程模型潜变量间效应值

路径	直接效应值	间接效应值	总效应
F2←F1	0.771	0.000	0.771
F3←F1	0.193	0.551	0.744
F4←F1	0.843	0.000	0.843
F3←F4	0.164	0.000	0.164
F3←F2	0.535	0.000	0.535

注：F1：传染病的基本知识与观念；F2：传染病的预防；F3：传染病的管理与治疗；F4：传染病的辨认

讨论

本研究以IDSHL的因子结构为依据^[1,2]，结合传染病健康素养的理论知识，设计SEM，检验模型与数据适配度，综合评价模型拟合效果。通过SEM量化计算，探讨传染病健康素养4个维度的相互关系。结果表明，模型整体适配度良好，SEM设计合理，理论模型与实际数据拟合度较高。

本研究整体模型配适度指标中，除2项绝对适配统计量（χ²、χ²/df）和1项AIC外，其他统计量均达适配标准。温忠麟等^[15]认为χ²值受样本量影响较大，当样本量>1 000时，检验水准α=0.000 1仍然不够小。黄芳铭^[9]和吴明隆^[8,10]指出χ²/df由于使用χ²值作为分子，因此该统计量值仍然受到样本量影响，当样本量过大时，自由度值也不足以对χ²值进行校正。本研究样本量为4 499，远远>1 000的界值，故不宜使用χ²值及χ²/df评价适配度。在判别模型是否可以接受时，应参考其他适配统计量，进行综合判断。CAIC值为考虑了样本量影响、校正后的AIC值，故宜使用CAIC而不是AIC评价适配度。

本研究中，4个潜变量之间的直接或间接作用，与之前的国内外的研究结果一致^[3,4,5,6,16]，即中国居民传染病的基本知识与观念水平对传染病的辨认、预防水平均有正向直接影响，而对传染病的管理与治疗既有直接影响，也有间接影响。但是以往的研究中，4个维度间的量化关系并未明确给出，而本研究使用SEM对传染病健康素养4个维度之间的关系进行了量化。结果表明，居民传染病的基本知识与观念的普及对传染病预防、管理与治疗、辨认水平的影响是明显的，且程度较大；其中，对传染病管理与治疗的影响路径较多，强度最大，间接效应较直接效应大。提示通过健康教育与健康促进的方法手段，不断改善居民传染病基本知识与观念、传染病的识别和预防技能，从而促进传染病管理与治疗水平的提高，是可行的。因此，传染病的基本知识与观念的改善情况应作为反映健康教育与健康促进工作效果的一个重要指标。

本研究只是分析了传染病健康素养4个维度之间的关系，各维度的外部影响因素，如社会人口学特征、历史性因素等，有待进一步探讨。

综上所述，本研究成功建立IDSHL量表4个维度的结构方程模型。模型整体适配度良好，SEM设计合理，理论模型与实际数据拟合度较高，可为我国开展传染病健康素养干预工作提供参考依据。

利益冲突

所有作者均声明不存在利益冲突

参考文献

[1]

TianXY，DiZQ，ChengYL，et al. Study on the development of an infectious disease-specific health literacy scale in the Chinese population[J]. BMJ Open，2016，6（8）：e012039. DOI：10.1136/bmjopen-2016-012039.

[2]

晋菲斐，田向阳，邸泽青，等.中国居民传染病健康素养量表编制与信效度检验[J].中国公共卫生，2016，32（12）：1651-1655. DOI：10.11847/zgggws2016-32-12-13.

JinFF，TianXY，DiZQ，et al. Development and evaluation of an infectious disease-specific health literacy scale[J]. Chin J Public Health，2016，32（12）：1651-1655. DOI：10.11847/zgggws2016-32-12-13.

[3]

YangP，DunzhuC，WiddowsonMA，et al. Infectious disease-specific health literacy in Tibet，China[J]. Health Promot Int，2018，33（1）：84-91. DOI：10.1093/heapro/daw054.

[4]

赵蕊晓，耿妍妍.健康教育在传染病预防控制中的效果分析[J].世界最新医学信息文摘，2017，17（57）：19-20. DOI：10.19613/j.cnki.1671-3141.2017.57.009.

ZhaoRX，GengYY. Effect analysis of health education in prevention and control of infectious diseases[J]. World Latest Med Inf，2017，17（57）：19-20. DOI：10.19613/j.cnki.1671-3141.2017.57.009.

[5]

陈晓芳.健康知识宣讲对传染病预防与控制的意义研究[J].中国医药指南，2013，11（4）：13-14. DOI：10.15912/j.cnki.gocm.2013.04.013.

ChenXF. The research of the significance of health knowledge preaching in the prevention and control for infectious disease[J]. Guide Chin Med，2013，11（4）：13-14. DOI：10.15912/j.cnki.gocm.2013.04.013.

[6]

马丽丽，孙丽双.健康教育在传染病预防控制中的应用分析[J].中国继续医学教育，2015，7（18）：221-222. DOI：10.3969/j.issn.1674-9308.2015.18.154.

MaLL，SunLS. Application of health education in the prevention and control of infectious diseases[J]. Chin Cont Med Educ，2015，7（18）：221-222. DOI：10.3969/j.issn.1674-9308.2015.18.154.

[7]

BavarianN，FlayBR，KetchamPL，et al. Using structural equation modeling to understand prescription stimulant misuse：a test of the Theory of Triadic Influence[J]. Drug Alcohol Depend，2014，138：193-201. DOI：10.1016/j.drugalcdep.2014.02.700.

[8]

吴明隆.结构方程模型——AMOS实务进阶[M].重庆：重庆大学出版社，2016：79-95.

WuML. Structural Equation Model－AMOS Practice Advanced[M]. Chongqing：Chongqing University Press，2016：79-95.

[9]

黄芳铭.结构方程模式：理论与应用[M].北京：中国税务出版社，2005：141-170.

HuangFM. Structural Equation Model：Theory and Application[M]. Beijing：China Tax Publishing House，2005：141-170.

[10]

吴明隆.结构方程模型——AMOS的操作与应用[M]. 2版.重庆：重庆大学出版社，2017：37-68，486-490.

WuML. Structural Equation Model－AMOS Practice and Application[M]. 2^nd ed. Chongqing：Chongqing University Press，2017：37-68，486-490.

[11]

SchumackerRE，LomaxRG. A Beginner’s Guide to Structural Equation Modeling[M]. 2^nd ed. Mahwah：Lawrence Erlbaum Associates，2004：85-104.

[12]

陆艳，徐华丽，魏骞，等.亚健康评定量表应用于城镇居民的验证性因子分析[J].中国全科医学，2013，16（13）：1108-1109，1112. DOI：10.3969/j.issn.1007-9572.2013.10.009.

LuY，XuHL，WeiQ，et al. Confirmatory factor analysis of sub-health measurement scale applied in urban residents[J]. Chin Gen Pract，2013，16（13）：1108-1109，1112. DOI：10.3969/j.issn.1007-9572.2013.10.009.

[13]

HairJF，BlackWC，BabinBJ，et al. Multivariate Data Analysis：a Global Perspective[M]. 7^th ed. New York：Prentice Hall，2009.

[14]

王晓康.结构方程模型在居民健康素养分析中的应用[D].南京：东南大学，2016.

WangXK. The application of structural equation modeling in the analysis of residents’ health literacy[D]. Nanjing：Southeast University，2016.

[15]

温忠麟，侯杰泰，马什赫伯特.结构方程模型检验：拟合指数与卡方准则[J].心理学报，2004，36（2）：186-194.

WenZL，HouJT，MarshHW. Structural equation model testing：cutoff criteria for goodness of fit indices and chi-square test[J]. Acta Psychol Sin，2004，36（2）：186-194.

[16]

KeddyKH，SmithAM，SookaA，et al. The burden of typhoid fever in south Africa：the potential impact of selected interventions[J]. Am J Trop Med Hyg，2018，99（3Suppl）：55-63. DOI：10.4269/ajtmh.18-0182.

贡献者信息

胡佳

中国疾病预防控制中心，北京　100011；中国健康教育中心培训部，北京　100011

田向阳

中国健康教育中心培训部，北京　100011

陈继彬

中华预防医学会报刊管理部，北京　100011

任学锋

中国健康教育中心培训部，北京　100011

程玉兰

中国健康教育中心培训部，北京　100011

通信作者

田向阳

中国健康教育中心培训部，北京　100011

Email：healthtian@163.com

关键词

传染病健康素养测评量表; 结构方程模型;

基金项目

国家科技支撑计划（2013BAI06B06）

利益冲突

所有作者均声明不存在利益冲突

历史

出版日期：2019-02-10

收稿日期：2018-09-03

本文编辑

万玉立

Learning-Discovery-Communication

Structural equation model analysis of infectious disease-specific health literacy scale in China

Hu Jia, Tian Xiangyang, Chen Jibin, Ren Xuefeng, Cheng Yulan

Published 2019-02-10

Cite as Chin J Epidemiol, 2019, 40(2): 237-240. DOI: 10.3760/cma.j.issn.0254-6450.2019.02.021

Abstract

Objective

To explore the relationship between different dimensions of infectious disease-specific health literacy scale in China.

Methods

Structural equation model (SEM) was employed to assess the psychometric properties of the infectious disease-specific health literacy scale. Based on the database from a randomly selected sample of 4 499 adult residents in three provinces in China, from March to May 2015. AMOS 21.0 software was used to build the SEM for data analyses.

Results

SEM analyses showed a good model fit of data, with the following satisfied parameters: goodness-of-fit index was 0.969, adjusted goodness-of-fit index was 0.962, root mean square residual was 0.038, root mean square error of approximation was 0.038, standardized root mean square residual was 0.032, Tacker-Lewis index/non-normed fit index was 0.926, comparative fit index was 0.934, normed fit index was 0.925, relative fit index was 0.915, incremental fit index was 0.934, parsimony goodness-of-fit index was 0.782, parsimony-adjusted normed fit index was 0.817, parsimony-adjusted comparative fit index was 0.825 and critical N was 702. The established SEM showed that the total influence path coefficient of "infectious disease-related knowledge and values" on the "infectious disease prevention" , "management or treatment of infectious diseases" and "identification of infection sources" were 0.771, 0.744 and 0.843, respectively. The total influence path coefficients of "identification of infection sources" , "infectious disease prevention" on "management or treatment of infectious diseases" were 0.164 and 0.535, respectively. The effect of "infectious disease-related knowledge and values" on "management or treatment of infectious diseases" appeared the greatest (55.4%), followed by "infectious disease prevention" (28.6%) and "identification of infection sources" (2.7%).

Conclusion

This SEM could be optimistically used for planning and evaluation of health education and promotion programs on infectious diseases prevention.

Key words:

Infectious disease-specific health literacy scale; Structural equation model

Contributor Information

Hu Jia

Chinese Center for Disease Control and Prevention, Beijing 100011, China

Chinese Center for Health Education, Beijing 100011, China

Tian Xiangyang

Chinese Center for Health Education, Beijing 100011, China

Chen Jibin

Chinese Preventive Medicine Association, Beijing 100011, China

Ren Xuefeng

Chinese Center for Health Education, Beijing 100011, China

Cheng Yulan

Chinese Center for Health Education, Beijing 100011, China

共有条评论

验证码

本文被引情况 CSCD: 0次万方数据： 0次 Scopus: 0次

施引文献(最多仅列5条文献，进入CSCD官网发现更多)

未获取施引文献信息...

暂无相关资源