孟德尔随机化方法，遵循孟德尔遗传定律，"亲代等位基因随机分配给子代"，以遗传变异作为工具变量，以此推断观察性研究中暴露因素与研究结局的因果关联。近年来，随着全基因组关联研究（GWAS）及各种组学数据的飞速发展，大量汇总数据的公开，为孟德尔随机化方法在因果推断中的广泛应用提供契机。本文针对目前常用的三种孟德尔随机化方法进行阐述，并将其应用于探索血液代谢物与抑郁症的因果关联，比较三种方法在因果推断的优缺点，以期为孟德尔随机化在观察性研究中的应用提供参考。
版权归中华医学会所有。
未经授权，不得转载、摘编本刊文章，不得使用本刊的版式设计。
除非特别声明，本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
随机对照试验（randomized controlled trail，RCT）是流行病学研究中进行因果推断的金标准[1]。然而由于医学伦理、受试者选择约束、结果外推性差等问题，实际工作中有些RCT往往难以开展。相比之下，观察性研究因其设计相对简单且易于实施，被广泛应用于病因的初步探索[2,3,4]。但由于反向因果关联、潜在的混在因素等问题，观察性研究结果往往存在争议，且不能被实验性研究所证实，因此在病因推断方面饱受质疑[5,6,7]。近年来，孟德尔随机化（mendelian randomization，MR）方法的提出，为解决上述问题提供了有效的途径[8,9]。
孟德尔随机化方法的基本思想是：利用与暴露因素具有强相关的遗传变异（genetic variation）作为工具变量（instrumental variable，IV），借此推断暴露因素与研究结局之间的因果效应[10]。根据孟德尔遗传规律，亲代的等位基因随机分配给子代，此过程相当于RCT中的随机分组过程[11]。因此，若遗传变异与混杂因素无关但与暴露因素有关，且遗传变异通过暴露因素对研究结局产生影响，则可以用遗传变异来推断暴露因素与研究结局之间的因果效应。由于遗传变异与生俱来，遗传变异与结局的关联符合因果时序关系，且不会受到后天的环境因素、社会因素等常见的混在因素的干扰，因此利用MR方法对观察性研究进行因果推断已经成为目前的研究热点[12,13,14]。近年来，随着全基因组关联研究（genome-wide association study，GWAS）及各种组学数据的飞速发展，大量汇总数据的公开共享[15,16,17]，为MR方法在探索复杂暴露因素与疾病结局因果关联中的广泛应用提供契机。由于单个遗传变异所能解释的变异有限，检验效能不高；且在GWAS研究背景下，往往有多个遗传变异与目标表型相关，因此采用多个遗传变异作为工具变量，可明显提升MR方法的检验效能[18,19]。本文将对目前常用的几种基于汇总数据的多工具变量MR方法进行的阐述，并利用这些方法探索血液中代谢物与抑郁症的因果关联，为MR方法在观察性研究中的应用提供参考。
IVW是由Burgess等[20,21]提出的，用于多工具变量的MR研究中。
不妨记G={G1，G2，…GJ}为工具变量，X为暴露因素，Y为结局变量。假设第j个工具变量（Gj）对暴露因素和结局的效应分别为
和
，其对应的标准误为
和
，则可通过比值法得到相应的因果效应值：
，标准误为
。然后选择固定效应模型或随机效应模型将
进行整合，最终得到暴露因素与结局的因果效应值
。
当工具变量之间是独立时：
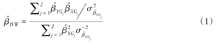
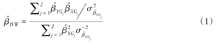
渐近标准误为：
。以
作为权重，则可通过加权线性回归，强制线性回归的截距项为0，即：
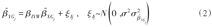
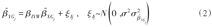
得到相应的因果效应值估计为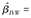
，其中V是工具变量的方差矩阵。当工具变量之间存在相关时，因果效应估计值为：
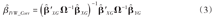
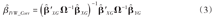
其中Ω为工具变量间的方差-协方差矩阵：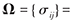
，相应的标准误为
。
当工具变量存在多效性问题时，采用IVW会导致因果效应估计出现偏差。针对此问题，Bowden等[22]对IVW进行修正，提出了MR-Egger。与IVW强制线性回归的截距项为0的做法不同，MR-Egger通过截距项来衡量工具变量间的平均多效性，其加权回归方程如下：
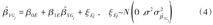
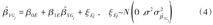
MR-Egger弱化了传统孟德尔随机化方法对工具变量排他性假设：工具变量与结局无关，且仅通过暴露因素影响结局。MR-Egger仅需满足工具变量与结局的直接效应独立于工具变量与暴露因素的关联效应（instrument strength independent of direct effect，InSIDE）假设。当InSIDE假设满足时，MR-Egger可得到因果效应的一致性估计值，其截距项β0E可解释为J个遗传变异的平均多效性的估计值[22]。若截距项为0，则MR-Egger即退化为IVW；若截距项不为0，则说明存在多效性，或者违背InSIDE假设。因此，可以通过MR-Egger的截距项对工具变量的假设进行有效的评估。
GSMR[23]是基于汇总数据的孟德尔随机化法（summary data-based mendelian randomization，SMR）[24]的扩展，利用工具变量之间的相关关系构建
的方差-协方差结构，并以此作为权重，最终通过广义线性模型求解总的因果效应值。
每个工具变量估计的效应值为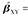
，其中效应值之间的方差-协方差矩阵M非对角线上元素为：
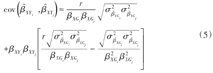
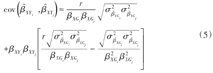
对角线上元素为：
通过广义最小二乘法可估计得因果效应为
，相应的方差为
。同时，GSMR提供工具变量异质性检验的方法（heterogeneity in dependent instrument，HEIDI）用于识别多效性，将存在多效性的工具变量筛选出来并剔除，从而得到因果效应的一致性估计值。当工具变量只有一个时，GSMR退化为SMR。
三种常用的基于汇总数据的多工具变量MR方法均需满足针对工具变量的假设才能得到因果效应的无偏估计值。实际应用中，需要根据汇总数据的真实情况，选择合适的方法，才能得到准确无偏的因果效应估计值。三种方法的共同点及区别如表1所示。
三种孟德尔随机化方法的比较
三种孟德尔随机化方法的比较
| IVW | MR-Egger | GSMR | |
|---|---|---|---|
| 原理 |  与 的加权线性回归，且强制截距项为0 |  与 的加权线性回归 |  的广义最小二乘法 |
| R包函数 | mr_ivw函数［25］ | mr_egger函数［25］ | gsmr函数［23］ |
| 应用条件 | 工具变量满足关联性、独立性以及排他性假设 | 工具变量满足关联性、独立性和InSIDE假设 | 工具变量满足关联性、独立性以及排他性假设 |
| 优点 | 在工具变量不存在多效性时，估计精度高、检验效能高 | 工具变量存在多效性时，仍能得到无偏估计；可通过截距项衡量平均多效性；可用做敏感性分析 | 在工具变量不存在多效性时，估计精度高、检验效能高；可通过HEIDI检验工具变量是否存在多效性 |
| 缺点 | 工具变量存在多效性时，估计有偏 | InSIDE假设不满足时，估计有偏，且一类错误膨胀；不存在多效性时，检验效能低于IVW和GSMR | 工具变量存在多效性时，估计有偏 |
| 注意事项 | 分析前需先删除多效性的工具变量 | 分析中需要保证所有工具变量的方向是一致的 | 分析前需先用HEIDI检验删除多效性的工具变量 |
| 三种方法共同注意事项：MR方法要求汇总数据来自于同质人群，或汇总数据校正过人群结构的；MR方法需要大样本才能达到足够的把握度；估计精度和检验效能取决于工具变量所能解释的变异度。 | |||
注：IVW：逆方差加权法；MR-Egger：基于Egger回归的孟德尔随机化法；GSMR：基于汇总数据的广义孟德尔随机化法；InSIDE：工具变量与结局的直接效应独立于工具变量与暴露因素的关联效应；HEIDI：工具变量异质性检验
抑郁症是一种以反复发作，持久的心境低落并伴随躯体症状为主要临床特征的情绪精神障碍，在不同的人身上有不同的表现、病因和发病机制[26]。重度抑郁症会导致患者生活质量明显降低，社会功能减弱，身体健康状况不佳，目前已经成为发达国家和发展中国家人群致残的重要原因之一，预计在未来十年内，将成为仅次于心血管系统疾病的第二大严重危害人类健康的疾患[27]。目前，抑郁症在我国的发病率为3.0%~5.0%，大约有6 100万抑郁症患者[28]。尽管目前关于抑郁症的全基因组关联研究已经发现一些遗传易感位点[29]，但抑郁症的发病机制尚不清楚，且由于混杂因素的存在，为其病因探索带来挑战。
代谢组学可以定量描述生物体内源性代谢物质的整体变化情况及其对内、外因刺激的应答规律，探讨生物体的代谢途径、特征及规律。本研究利用孟德尔随机化方法，基于代谢物数量性状位点（metabolites quantitative trait locus，mQTL）研究的汇总数据以及抑郁症GWAS的汇总数据，探索血液中代谢物水平与抑郁症的因果关联，为揭示抑郁症的发病机制以及后期的实验性研究提供参考依据。
mQTL汇总数据来源于Shin等[16]在2014年Nature Genetics上发表的关于人类血液代谢产物的研究（http://metabolomics.helmholtz-muenchen.de/gwas/），其中529种代谢物满足P<1×10-5。抑郁症GWAS汇总数据来源于180 866名人群Meta分析的结果[29]（https://www.thessgac.org/data），整合了精神病学基因组学联盟（Psychiatric Genomics Consortium，PGC）、英国生物数据库（UK Biobank，UKB）以及老年遗传流行病学研究（Genetic Epidemiology Research on Aging，GERA）的关联分析结果。
数据处理和分析采用R软件，其中GSMR使用gsmr包，IVW和MR-Egger采用Mendelian Randomization包。分析流程如图1所示。最终筛选出9 135个SNP作为工具变量，包含253种代谢物。以SNP间连锁不平衡（linkage disequilibrium，LD）大于0.2为标准，剔除存在高LD的SNP，后分别采用GSMR、IVW和MR-Egger探索每种代谢物与抑郁症之间的因果关联，结果如表2所示。
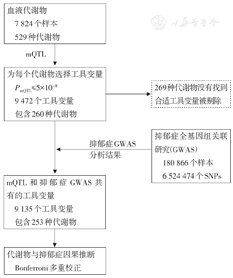
mQTL：基于代谢物数量性状位点研究；GWAS：全基因组关联研究；PmQTL：基于代谢物数量性状研究的P值
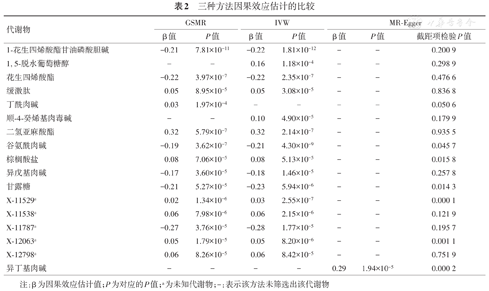
三种方法因果效应估计的比较
三种方法因果效应估计的比较
| 代谢物 | GSMR | IVW | MR-Egger | ||||
|---|---|---|---|---|---|---|---|
| β值 | P值 | β值 | P值 | β值 | P值 | 截距项检验P值 | |
| 1-花生四烯酸酯甘油磷酸胆碱 | -0.21 | 7.81×10-11 | -0.22 | 1.81×10-12 | - | - | 0.200 9 |
| 1, 5-脱水葡萄糖醇 | - | - | 0.16 | 1.18×10-4 | - | - | 0.298 9 |
| 花生四烯酸酯 | -0.22 | 3.97×10-7 | -0.22 | 2.35×10-7 | - | - | 0.476 6 |
| 缓激肽 | 0.05 | 8.95×10-5 | 0.05 | 3.08×10-5 | - | - | 0.836 8 |
| 丁酰肉碱 | 0.03 | 1.97×10-4 | - | - | - | - | 0.050 6 |
| 顺-4-癸烯基肉毒碱 | - | - | 0.10 | 4.90×10-5 | - | - | 0.179 9 |
| 二氢亚麻酸酯 | 0.32 | 5.79×10-7 | 0.32 | 2.14×10-7 | - | - | 0.935 5 |
| 谷氨酰肉碱 | -0.19 | 3.62×10-7 | -0.21 | 4.30×10-9 | - | - | 0.045 7 |
| 棕榈酸盐 | 0.08 | 7.06×10-5 | 0.08 | 5.13×10-5 | - | - | 0.015 8 |
| 异戊基肉碱 | -0.17 | 3.60×10-5 | -0.18 | 1.46×10-5 | - | - | 0.257 8 |
| 甘露糖 | -0.21 | 5.27×10-5 | -0.23 | 5.94×10-6 | - | - | 0.014 3 |
| X-11529a | 0.02 | 1.34×10-6 | 0.03 | 2.55×10-7 | - | - | 0.000 1 |
| X-11538a | 0.06 | 7.98×10-6 | 0.06 | 2.15×10-6 | - | - | 0.121 9 |
| X-11787a | -0.27 | 3.76×10-5 | -0.28 | 1.77×10-5 | - | - | 0.195 7 |
| X-12063a | 0.05 | 1.79×10-5 | 0.05 | 8.20×10-6 | - | - | 0.001 1 |
| X-12798a | 0.06 | 8.26×10-5 | 0.06 | 8.42×10-5 | - | - | 0.751 9 |
| 异丁基肉碱 | - | - | - | - | 0.29 | 1.94×10-5 | 0.000 2 |
注：β为因果效应估计值；P为对应的P值；a为未知代谢物；-：表示该方法未筛选出该代谢物
从表2可以看出：GSMR和IVW在因果推断的表现上很接近。GSMR筛选出14个代谢物满足Bonferroni校正标准（P≤ 0.05/253），而IVW筛选出15个代谢物，且其中有13个代谢物在两种方法中都筛选出来，因果效应估计值也基本一致。对于13个重叠的代谢物，由MR-Egger截距项的P值可知，有5个代谢物P<0.05，说明工具变量可能存在多效性，此时GSMR和IVW的估计结果可能有偏，且MR-Egger分析结果并未筛选出这5个代谢物，意味着GSMR和IVW因果推断可能存在假阳性。因此针对这5个代谢物与抑郁症的因果关联需要进一步的数据验证。MR-Egger的检验效能明显低于上述两种方法，仅筛选出1个代谢物，且该结果未被另外两种方法验证。MR-Egger截距项的P值提示，该代谢物的工具变量存在多效性，因此GSMR和IVW并未筛选出该代谢物。
MR是一种灵活、稳健的控制混杂的统计方法，近年来随着GWAS及各种组学技术的不断发展，为MR研究暴露因素与复杂疾病之间的因果关联提供了广阔的基础。MR方法提供的因果关联证据强度介于干预性研究和观察性研究之间，可以有效地避免混杂和反向因果关系所带来的偏倚，发现更为可靠的证据来指导干预性研究，且可在随机对照试验无法实施的情况下提供强有力的证据[30]。本研究的结果表明，IVW法和GSMR在因果关联推断上的表现相似，其本质上对每个工具变量估计出的效应值拟合一条过原点的最佳直线，直线的斜率即为因果效应的估计值，无法校正多效性问题，在分析前需要将存在多效性的遗传变异剔除，否则会导致估计结果有偏倚。MR-Egger利用无约束的截距项来衡量平均多效性，可以校正由于多效性带来的偏倚，因此即使是在存在多效性问题的情况下，MR-Egger仍然能得到因果效应的一致性估计值。尽管MR-Egger在多效性问题上凸显出其优势，但研究表明，MR-Egger的估计标准误一般大于IVW，而在检验效能方面的表现则要逊色于IVW[31]。三种方法各有优缺点，需根据实际数据情况选择合适的方法进行分析。
与大多数的流行病学方法一样，MR方法也要依赖于一些假设，当且仅当这些假设都满足时，孟德尔随机化才能得到准确可靠的结论。因此，在MR分析中，有几点问题需要注意：（1）弱工具变量问题：MR方法的检验效能高低与工具变量与暴露因素之间的关联强度密切相关，弱工具变量会导致结果出现偏差；（2）多效性问题：当工具变量存在多效性问题，其因果推断的结论解释需谨慎，需要采用不同的方法进行分析，以期得到稳健的结果；（3）把握度低问题：MR分析往往需要大样本数据才能达到足够的把握度，可整合公共数据库中基于大样本的汇总数据进行因果推断；（4）设计所带来的混杂问题：在病例-对照研究中，由于其设计本身会引入一些混杂，导致工具变量与混杂之间的独立性假设不成立，对于此类数据的MR分析需要寻求合适的解决策略[32]；（5）效应值方向问题：两阶段MR分析中，需要确保工具变量-暴露以及工具变量-结局关联分析中效应等位基因（effect allele）是一致的；（6）人群异质性问题：两阶段MR分析中，需保证工具变量-暴露以及工具变量-结局关联分析汇总是来自于同质的人群，或校正过人群结构，否则会导致估计有偏。
综上所述，笔者建议：（1）实际应用时，先用MR-Egger检验是否存在多效性；在不存在多效性时，采用IVW和GSMR进行分析，两种方法的结果一致时，结论更可靠。（2）审慎解读分析结果。由于复杂疾病的发生发展过程涉及基因组、转录组、代谢组等不同层次的生物学过程，而目前对这些生物学过程的认识尚且不足，使得MR方法得到的因果关联结果常常缺乏合理的生物学解释，在应用上还存在一定的局限性。若从生物学机制上已明确，暴露在前，结局发生在后，遗传变异通过改变暴露水平从而导致结局发生，则可通过MR方法排除已知或未知混杂的干扰，确定暴露因素与结局的因果效应大小。但在某些情况下无法明确是暴露导致结局发生还是结局改变了暴露水平（如遗传变异与BMI和C-反应蛋白均有关，但无法确定是BMI水平改变导致C-反应蛋白水平改变，还是C-反应蛋白水平改变影响BMI水平[33]），则MR方法无法识别此类因果关联方向[34]，需要通过双向MR方法进一步剖析暴露因素与结局因果关联的方向。若双向MR均显示有统计学意义，则说明暴露既是"因"又是"果"。
总之，孟德尔随机化方法的应用为传统的观察性流行病学研究提供新思路，为病因推断提供更强有力的证据，为后期的进一步实验性验证研究提供参考依据。
所有作者均声明不存在利益冲突
