
倾向性评分作为一种对多个协变量进行调整的分析策略,在观察性疗效比较研究中的应用越来越广泛。本文从基本原理、案例分析、软件实现等方面对该方法进行详细介绍,以期读者对倾向性评分方法有所了解,在科研工作中能正确应用,提高数据使用效率和统计分析水平。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
随机对照试验(randomized controlled trial,RCT)采用随机分配的方法,将合格研究对象分别分配到试验组和对照组,并接受相应的试验措施,在一致的条件下或环境中,同步地进行研究和观测试验效应。RCT被公认为是治疗性研究的最佳设计方案,能够得到干预措施在理想状态下所能达到的理论疗效(efficacy),但并不适用于所有的临床研究和解决所有的临床问题[1,2],例如疾病预后的自然病史,干预措施在现实世界中的实际效果(effectiveness)的评价等。近年来,非随机对照的观察性疗效比较研究(comparative effectiveness research)得到了前所未有的重视[3]。
然而在此类研究中,由于缺乏随机化,混杂偏倚的控制尤为重要。混杂因素(confounder)又称外来因素(extraneous factor),与干预因素和研究结局皆相关,但不是暴露-结局的因果关系通路上的中间变量,该因素的存在将歪曲(夸大或缩小)暴露因素和结局的真实关联。非随机对照研究应密切关注潜在混杂因素,采用适当的设计和分析方法,尽可能地控制混杂效应,控制偏倚,使混杂因素的影响达到最小。
对于已知且已测量的混杂因素,除了传统的分层分析、配对分析、协方差分析和多因素分析,PS作为一种对多个协变量进行调整的分析策略,在观察性疗效比较研究中的应用越来越广泛。
PS由Rosenbaum和Rubin[4]于1983年首次提出。它是多个协变量的一个函数,用于处理观察性研究中组间协变量分布不均衡的问题。PS是根据已知协变量的取值(Xi)而计算的第i个个体分入观察组的条件概率:
e(X)=P(G=1|X)
这里G表示组别或干预因素,G=1表示该个体在观察组,G=0表示该个体在对照组;X为协变量向量X=(x1,x2,…,xm)。假定个体i所在组别与协变量无关,即分组变量G与协变量X相互独立,若PS用传统的logistic回归或probit回归方法计算,即以组别G为因变量,以所要控制的因素为自变量建立logistic模型:
logit[P(G=1|X)]=α+β1x1+…+βmxm
或probit模型:
Φ-1(P(G=1|X))=α+β1x1+β2x2+...+βmxm
Φ为正态累积概率函数。将每个个体的协变量取值代入模型中,即可估计得到该个体的PS:
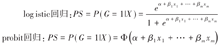
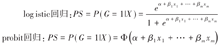
可见,PS是给定协变量X的条件下,个体接受干预(G=1)的概率估计。研究表明,PS模型变量的选择标准应该是纳入所有与结局有关的协变量,具体应结合相关学科专业知识进行选择[5]。
PS法本身不能控制混杂,而是通过匹配、分层、或进入回归模型直接调整混杂等方式,不同程度地提高对比组间的均衡性,从而削弱或平衡协变量对效应估计的影响,达到"类随机化"的效果,又称为事后随机化[6]。
如果将PS相同或相近的研究对象在不同的组间进行匹配,理论上,组间各特征变量的分布将趋于均衡,从而削弱或抵消组间混杂因素的不均衡性对研究结果的干扰,这就是PS匹配法。从匹配范围上,倾向指数匹配法可分为局部匹配(local algorithms)和全局匹配(global algorithms),常用的局部匹配方法有最邻近匹配(nearest neighbor matching)、卡钳匹配(caliper matching)。将观察组中的每个个体,在对照组中寻找与其最接近的个体进行匹配,直到观察组中每个个体都找到匹配,称为最邻近匹配。如果两个个体的PS差值在事先设定的某范围(称为卡钳值(caliper))内才能进行匹配,称为卡钳匹配。卡钳值的设定直接影响到最终匹配集的样本量,卡钳值越大,能够匹配成功的个体越多,匹配集就越大,但是对比组间的均衡性可能较差;反之,卡钳设置过小,虽然可提高对比组间的均衡性,但匹配成功率可能降低,匹配集的样本量减少。Austin的蒙特卡洛模拟结果表明,最合适的卡钳值是取两组倾向指数标准差的20%,或者取两组间PS绝对差值(卡钳值)为0.02或0.03等。此外,还有马氏距离法(mahalanobis),以及由其衍生的通用匹配法(genetic matching,GenMatch)等。而全局匹配法将匹配问题转化为运筹学中网络流问题(network flows),此时观察组和匹配的对照组个体PS差值并不是最小的,但是能保证匹配集PS总体差值的最小化[7]。
值得一提的是,PS匹配还需满足重叠假定(overlap assumption),即观察组和对照组的PS取值范围有相同的部分(common support),具体来说,若某观察个体的PS值明显高于对照组PS的最大值或明显低于对照组PS的最小值,则考虑去掉该观察个体。
将PS直接作为一个新的协变量进行模型校正,即在回归分析模型中,以结局变量为应变量,以分组变量为自变量,PS作为唯一协变量,来构建模型,估计组间效应,即为PS校正法。PS校正法没有损失样本,最大限度保留了原有信息,但PS校正是基于模型的分析,要求建模正确。
PS也可以作为分层变量,将受试者按照PS的大小分为若干区间,视区间为层,进行分层分析。所有的观察组和对照组中研究对象均参与分析,此时,层内组间协变量分布认为是均衡的,当层内有足够样本量时,可以直接对单个层进行分析。也可以对各层效应进行加权平均,作分层分析。当两组的PS评分分布偏离较大时,可能有的层中只有对照组个体,而有的层只有试验组的个体。此时,这些层不能提供信息。PS分层的关键问题是分层数和权重的设定。可通过比较层内组间PS的均衡性来检验所选定的层数是否合理,权重一般由各层样本占总样本量的比例来确定,也有学者建议采用各层内处理效应方差的倒数[8]。根据文献报道,按PS将样本平均分为5层,能减少90%以上的偏倚,是PS分层中最常用的方法[9]。
根据文献报道,在基于PS的方法中,基于PS的匹配法是目前高影响力的医学和公共卫生杂志中使用最多的方法,占三分之一,其次为PS校正。本文分别以匹配法和校正法为例演示PS法的实施和应用。
重症呼吸综合征(acute respiratory distress syndrome,ARDS)是ICU的常见重症之一,死亡风险较高,血小板与纤维蛋白原联合作用通过多种信号转导途径介导内皮损伤,是肺源性ARDS病理机制之一,本案例欲考察血小板减少与ARDS患者的死亡关联。
本案例数据来源于马萨诸塞州综合医院(Massachusetts General Hospital,MGH)和哈佛公共卫生学院的ARDS分子流行病学研究项目(Molecular Epidemiology of ARDS Study,MEARDS)中的ARDS病例。
病例的基本特征资料包括年龄、性别、种族、血小板基线、急性生理与慢性健康评分Ⅲ(acute physiology and chronic health evaluation,APACHE Ⅲ)、是否患脓毒血症、是否患急性肺炎、是否患白血病、是否患非霍奇金淋巴瘤、是否患实体肿瘤、是否患肝硬化、是否输血治疗、是否透析等,其中部分特征指标在两组间并不均衡,如性别、APACHE Ⅲ评分、是否输血治疗,见表1。
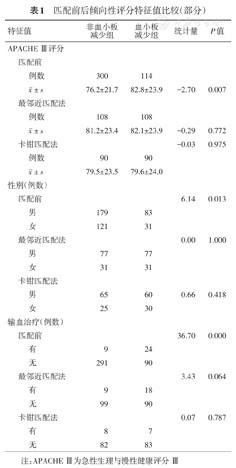
匹配前后倾向性评分特征值比较(部分)
匹配前后倾向性评分特征值比较(部分)
| 特征值 | 非血小板减少组 | 血小板减少组 | 统计量 | P值 | ||
|---|---|---|---|---|---|---|
| APACHE Ⅲ评分 | ||||||
| 匹配前 | ||||||
| 例数 | 300 | 114 | ||||
 ± s ± s | 76.2±21.7 | 82.8±23.9 | -2.70 | 0.007 | ||
| 最邻近匹配法 | ||||||
| 例数 | 108 | 108 | ||||
 ± s ± s | 81.2±23.4 | 82.1±23.9 | -0.29 | 0.772 | ||
| 卡钳匹配法 | -0.03 | 0.975 | ||||
| 例数 | 90 | 90 | ||||
 ± s ± s | 79.5±23.5 | 79.6±24.0 | ||||
| 性别(例数) | ||||||
| 匹配前 | 6.14 | 0.013 | ||||
| 男 | 179 | 83 | ||||
| 女 | 121 | 31 | ||||
| 最邻近匹配法 | 0.00 | 1.000 | ||||
| 男 | 77 | 77 | ||||
| 女 | 31 | 31 | ||||
| 卡钳匹配法 | ||||||
| 男 | 65 | 60 | 0.66 | 0.418 | ||
| 女 | 25 | 30 | ||||
| 输血治疗(例数) | ||||||
| 匹配前 | 36.70 | 0.000 | ||||
| 有 | 9 | 24 | ||||
| 无 | 291 | 90 | ||||
| 最邻近匹配法 | 3.43 | 0.064 | ||||
| 有 | 9 | 18 | ||||
| 无 | 99 | 90 | ||||
| 卡钳匹配法 | 0.07 | 0.787 | ||||
| 有 | 8 | 7 | ||||
| 无 | 82 | 83 | ||||
注:APACHE Ⅲ为急性生理与慢性健康评分Ⅲ
本案例将满足下列情形之一的ARDS病例定义为血小板减少组:基线血小板计数低于100×109个/L;治疗后14 d内血小板计数低于100×109个/L;治疗后14 d内血小板计数下降大于100×109个/L。将ARDS患者据此分为血小板减少组和非血小板减少组,血小板减少组114人,非血小板减少组300人。采用probit回归,以年龄、性别、种族、是否输血、APACHE Ⅲ评分建立模型,估计每个患者的PS值。考虑三种分析方法比较两组患者的住院28 d死亡率:(1)基于PS的最邻近匹配法:根据PS值,对血小板减少组的每个患者,将非血小板减少组中与之最接近的一个个体进行匹配,均衡两组基本特征后采用单因素logistic回归,比较两组患者住院28 d的死亡率;(2)基于PS的卡钳匹配法:根据PS的值,对血小板减少组的每个患者,将非血小板减少组中与之相差绝对值不超过0.03的患者进行匹配,如果有多个个体在卡钳值0.03范围内,则采取随机抽样方法抽取一个进行匹配,均衡两组基本特征后采用单因素logistic回归,比较两组患者住院28 d的死亡率;(3)基于PS的logistic回归校正法:将PS值作为唯一协变量,放入logistic回归模型加以校正,比较两组患者住院28 d的死亡率。
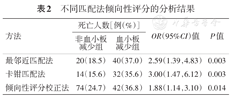
匹配前、最邻近匹配和卡钳匹配后两组PS分布见图1。匹配前APACHEⅢ评分、性别、输血治疗组间不均衡,匹配后均达到组间均衡,比较结果见表1。匹配后,最邻近匹配法成功获得108对,卡钳匹配成功获得90对。匹配后两组PS分布较匹配前均有所靠近。最邻近匹配法OR为2.59(95%CI:1.39~4.83),卡钳匹配法OR为3.00(95%CI:1.47~6.12),两种匹配方式结果相近。考虑到由于匹配失败带来的样本信息丢失,直接将PS值作为协变量纳入logistic模型后,依然得到两组死亡率有统计学差异的结果(P=0.014),OR值为1.88(95%CI:1.14~3.10)(表2)。因而,血小板低下的ARDS病例死亡风险较高,经最邻近匹配法、卡钳匹配法和PS校正法分析所得结论一致。
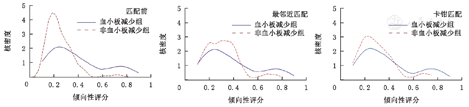

不同匹配法倾向性评分的分析结果
不同匹配法倾向性评分的分析结果
| 方法 | 死亡人数[例(%)] | OR(95%CI)值 | P值 | |
|---|---|---|---|---|
| 非血小板减少组 | 血小板减少组 | |||
| 最邻近匹配法 | 20(18.5) | 40(37.0) | 2.59(1.39,4.83) | 0.003 |
| 卡钳匹配法 | 14(15.6) | 32(35.6) | 3.00(1.47,6.12) | 0.003 |
| 倾向性评分校正法 | 74(24.7) | 42(36.8) | 1.88(1.14,3.10) | 0.014 |
PS法应用广泛,软件工具成熟,R(2.6.0以上版本)软件提供了Matching、MatchIt程序包[10];Stata(14.0)软件提供了Pscore、Psmatch2程序包[11];SPSS的PS matching模块[12]均可以进行不同匹配方法的分析,当然也可通过SAS编程的方式,各类软件所提供的匹配方法有所不同,但最经典的最邻近匹配法和卡钳匹配法均可实现。
上述案例采用State14.0的Psmatch2程序包完成,主要程序如下:
Psmatch2程序包安装:
ssc install psmatch2
最邻近匹配法程序命令:
psmatch2 plate_g age gender ethnic multran scoretot,
out(plate)common noreplacement
卡钳匹配法程序命令:
psmatch2 plate_gage genderethnic multran scoretot,
out(plate)common neighbor(1)caliper(0.03)noreplacement
其中plate_g为分组变量(取值需为0或1),out(plate)定义结局变量,并不影响匹配,psmatch2可根据所得匹配组对该结局变量进行比较,其余变量age、gender、ethinic、multran、scoretot为所需匹配的协变量,common选项指定PS匹配需满足重叠假定,noreplacement表示采用无放回的匹配方式,neighbor选项设置匹配比例,默认为1∶1,如果要做1:n匹配可以在此修改,caliper选项设置卡钳值。psmatch2程序包还提供了马氏距离(mahalanobis matching)、核函数匹配(kernel matching)等其他匹配方法。本文案例不同匹配法结果近似,故不赘述。psmatch2默认采用probit回归模型,可通过logit选项指定采用logistic回归模型。值得注意的是,在应用psmatch2命令进行PS匹配前需先将数据随机排序。
执行psmatch2命令后自动产生了一系列新变量,根据模型所得PS值默认储存在_pscore变量中,可通过pscore(varname)选项对该变量进行更名,此变量可直接用于PS校正;_id为每个观察对象唯一的ID号;_treated表示观察对象是否为观察组;_n1表示观察对象被匹配到的对照组的_id(如果是1∶2匹配,还会生成_n2);_pdif表示已完成匹配的观察对象间概率值之差。可根据这些变量进行匹配后数据整理,随后统计分析。
另外,该程序包还提供了pstest命令,可对匹配前后进行均衡性检验,但仅适用于连续性变量,psgraph可图示匹配结果。为了更好地展示PS的分布,本文图1采用two way命令绘制。
理论上讲,如果PS模型纳入了所有影响结果的因素,则通过匹配后得到的结果与经过随机化得到的结果性质应该是相同的。但实际上这是不可能的,也无法证明。PS匹配仅均衡已知且已测量的协变量,而没有考虑未知因素的影响,也就谈不上均衡。另外,由于匹配是有条件的,总有一些人找不到匹配对象,通过PS匹配势必损失信息,降低人群的代表性,因此,当匹配例数明显小于两组最小样本量时,样本的代表性就成问题了。
PS匹配时,采用不同的匹配方法,选择不同的匹配协变量,可能得到的结果不同,需通过不同匹配方法的敏感性分析来验证PS匹配法的稳健性。与传统的协变量校正法相比,PS匹配在所需考虑的协变量较多时更为适用。
PS分层法和PS校正法的优势是没有丢失样本,而是充分利用了所有样本,最大限度地保留了原有信息。当组间PS分布位置相同,或稍微偏离时,采用PS校正可以得到较好的效果;但是,当组间的PS分布相互偏离较大时,将PS作为协变量进行调整是不合适的,因为此时的调整可能产生错误的估计值。本文的案例分析中,匹配前组间PS分布位置相同,PS校正法取得了较好的效果,案例中PS匹配法与PS校正法结论相同,有效验证了研究结论稳健性。
当然,这里介绍的这些方法只是不得已而为之的权宜之计,提供了在现有条件下能够做到的最好途径。事实上,随机化是统计推断的基础,随机对照研究和观察性研究是相辅相成的,彼此无法替代,而要发挥各自的优势,均需严谨的设计,严格的实施,正确的分析和恰如其分的解释。
所有作者均声明无利益冲突
1.倾向性评分的定义是:
A. PS是随机分组的概率
B. PS是协变量的分布概率
C. PS是个体接受干预(G=1)的概率估计
D. PS是给定协变量X的条件下,个体接受干预(G=1)的概率估计
2.关于PS法的描述中,以下不正确的是:
A. PS法是非随机对照研究中用于控制混杂偏倚的方法
B.通过PS匹配可均衡对比组间的已知且已测量协变量分布
C. PS法使得非随机化试验资料达到"类随机化"的效果,相当于事后随机化
D. PS法可取代随机对照设计
3.PS匹配法包含:
A.最邻近匹配
B.马氏距离匹配
C.卡钳匹配
D.以上都是
4.PS的计算可采用的模型
A. Cox比例风险模型
B. Weibull回归模型
C. Logistic回归模型
D.多元线性回归模型
5.在某个观察性疗效比较研究中,共需要考虑控制12个协变量,其中,未测量的变量有2个,已测量的变量有10个,这10个变量中又有4个协变量在两组是均衡的,而有6个协变量在两组不均衡。则用于计算PS的变量应该是:
A.全部12个协变量
B. 10个已测量的协变量
C. 6个不均衡的协变量
D. 4个均衡的协变量



























