在确定研究因素与疾病结果间的关联时，如果结果变量（因变量）为连续变量，一般采用多重线性回归（multiple linear regression，MLR），如腰围、遗传因素、体重指数（body mass index，BMI）与血压的关系。MLR主要用于探讨自变量与连续因变量的关联，确定自变量的相对贡献大小和进行预测分析。MLR分析的自变量可以为连续变量，如年龄、收入和身高等；分类变量，如职业、血型和婚姻状况等；等级变量，如病情的轻、中、重。在拟合MLR时，按变量类型和专业知识，确定自变量以何种形式纳入模型：分类变量以哑变量的形式进入模型；连续变量以线性（原变量值）或分组线性引入模型；等级变量以分组线性或哑变量的形式进入模型。

MLR的模型为：Y_i=α+β₁X_i1+β₂X_i2+…+β_kX_ik+ε_i，上述公式为总体回归方程，i代表个体，α为截距项（常数项），X₁, X₂,…, X_k代表回归模型的k个自变量，β₁, β₂,…, β_k为相应自变量的回归系数，ε_i为误差项（残差项）。用实际数据拟合MLR，其样本回归方程为：_i =a+b₁X_i1+b₂X_i2+…+b_kX_ik，式中，_i，a，b₁, b₂,…, b_k为总体回归方程相应参数的估计值。

模型中各参数的估计方法和解释，拟合MLR的线性、独立、正态和方差齐性应用条件的检验可参考文献[1,2]。

多重线性回归要求结果变量为连续变量，如某现况调查，要探讨性别、年龄、胆固醇、BMI、腰围与血压的关联；这里自变量年龄、胆固醇、BMI、腰围与因变量血压要求为线性关系，这是拟合MLR的条件之一。简单的方法是以BMI（腰围、胆固醇或年龄）为横坐标，血压为纵坐标，作散点图，确定线性关系是否存在。当两者的线性关系不存在或不是很强时，可对自变量、因变量或两者都进行对数转换，使自变量与因变量的线性关系成立或近似成立。另外，医疗费用、死亡率、生存率、国内生产总值（gross domestic product，GDP）和住院天数的分布一般不为正态分布，可通过对数变换使之正态化。对数转换是个单调过程，它不改变x与y的方向，且原值（x）与转换后的值f(x)的大小顺序不变。在统计分析中，多采用以e为底的自然对数转换，即f(x)=log_e(x）。

以总体简单线性回归（simple linear regression，SLR）为例，其公式为：Y_i=α+βX_i+ε_i，X与Y均为连续变量，这里可能有三种取自然对数形式：X取对数、Y取对数、X与Y同时取对数，分别称为linear-log转换、log-linear转换和log-log转换，对应的样本SLR方程为：_i =a+blog_e(X_i)；log_e(_i)=a+bX_i；log_e(_i)=a+blog_e(X_i)。

注意，这里使用的是以e为底的自然对数，e≈2.718 281 828。下面以实例说明三种变换的应用场景和条件，如何判定该对哪些变量进行自然对数的转换。

例1：我国2016年50个地级市人均地区生产总值（per capita gross regional product，PCGRP）和其城镇人口比重（urban population proportion，UPP）见表1，以人均地区生产总值为自变量，城镇人口比重为因变量，进行线性回归分析。

点击查看表格

表1

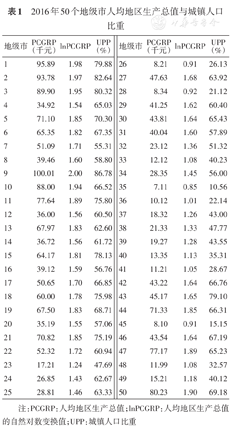
2016年50个地级市人均地区生产总值与城镇人口比重

表1

2016年50个地级市人均地区生产总值与城镇人口比重

地级市	PCGRP（千元）	lnPCGRP	UPP(%)	地级市	PCGRP（千元）	lnPCGRP	UPP(%)
1	95.89	1.98	79.88	26	8.21	0.91	26.13
2	93.78	1.97	82.64	27	47.63	1.68	63.92
3	89.90	1.95	80.32	28	8.34	0.92	21.12
4	34.92	1.54	65.03	29	41.25	1.62	60.40
5	71.10	1.85	70.30	30	43.81	1.64	65.43
6	65.35	1.82	67.35	31	40.04	1.60	57.89
7	51.09	1.71	55.31	32	23.12	1.36	51.32
8	39.46	1.60	58.80	33	12.12	1.08	40.23
9	100.01	2.00	86.78	34	28.35	1.45	56.00
10	88.00	1.94	66.52	35	7.11	0.85	10.56
11	77.64	1.89	75.80	36	10.12	1.01	22.14
12	36.00	1.56	60.50	37	18.32	1.26	43.00
13	67.97	1.83	62.60	38	21.33	1.33	47.77
14	36.72	1.56	61.72	39	19.27	1.28	43.55
15	64.17	1.81	78.13	40	13.35	1.13	35.31
16	39.12	1.59	56.76	41	11.21	1.05	28.67
17	50.65	1.70	66.85	42	43.22	1.64	66.76
18	60.00	1.78	75.98	43	45.17	1.65	79.10
19	67.50	1.83	68.71	44	71.33	1.85	66.31
20	35.19	1.55	57.06	45	8.10	0.91	15.15
21	70.82	1.85	75.19	46	43.54	1.64	67.19
22	52.32	1.72	60.94	47	77.17	1.89	65.23
23	17.21	1.24	47.69	48	11.99	1.08	32.57
24	26.85	1.43	62.67	49	15.21	1.18	40.12
25	28.81	1.46	63.33	50	80.23	1.90	69.18

注：PCGRP：人均地区生产总值；lnPCGRP：人均地区生产总值的自然对数变换值；UPP：城镇人口比重

以PCGRP为横坐标，UPP为纵坐标，其散点图见图1A；以lnPCGRP为横坐标，UPP为纵坐标，其散点图见图1B。图1A可见，随着PCGRP的增加，UPP也增加，但PCGRP值低时，UPP上升的比较快，呈现一个指数上升的趋势，而非线性。将PCGRP取自然对数后，图1B可见，lnPCGRP与UPP呈现一个线性增加的趋势，即正相关关系。

点击查看大图

图1

2016年50个地级市人均地区生产总值和其自然对数与城镇人口比重的散点图　图1A横坐标为人均地区生产总值；图1B横坐标为人均地区生产总值的自然对数值

点击查看大图

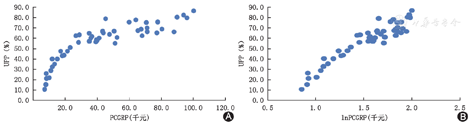
PCGRP：人均地区生产总值；UPP：城镇人口比重

图1

2016年50个地级市人均地区生产总值和其自然对数与城镇人口比重的散点图　图1A横坐标为人均地区生产总值；图1B横坐标为人均地区生产总值的自然对数值

例2：上述例1资料，以UPP为自变量，PCGRP为因变量，进行线性回归分析。以UPP为横坐标，PCGRP为纵坐标，其散点图如图2A；以UPP为横坐标，lnPCGRP为纵坐标，其散点图如图2B。图2A可见，随着UPP的增加，PCGRP也增加，但UPP值高时，PCGRP上升的比较快，呈现一个指数上升的趋势，而非线性。将PCGRP取自然对数后，图2B可见，UPP与lnPCGRP呈现一个线性增加的趋势，即正相关关系。

点击查看大图

图2

2016年50个地级市城镇人口比重与人均地区生产总值和其自然对数的散点图　图2A纵坐标为人均地区生产总值；图2B纵坐标为人均地区生产总值的自然对数值

点击查看大图

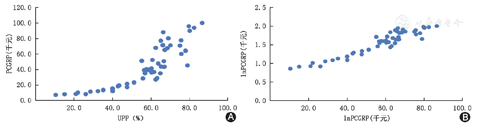
PCGRP：人均地区生产总值；UPP：城镇人口比重

图2

2016年50个地级市城镇人口比重与人均地区生产总值和其自然对数的散点图　图2A纵坐标为人均地区生产总值；图2B纵坐标为人均地区生产总值的自然对数值

例3：某省肿瘤医院总结随访了10年来曾在该医院住院手术的乳腺癌患者715例，每年的生存情况见表2。试以术后生存时间（YEAR）为自变量，生存率（SURVIVAL）为因变量，进行线性回归分析。

点击查看表格

表2

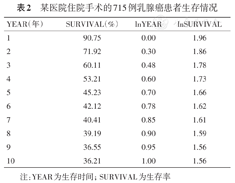
某医院住院手术的715例乳腺癌患者生存情况

表2

某医院住院手术的715例乳腺癌患者生存情况

YEAR（年）	SURVIVAL(%)	lnYEAR	lnSURVIVAL
1	90.75	0.00	1.96
2	71.92	0.30	1.86
3	60.11	0.48	1.78
4	53.21	0.60	1.73
5	45.23	0.70	1.66
6	42.12	0.78	1.62
7	40.41	0.85	1.61
8	39.19	0.90	1.59
9	36.55	0.95	1.56
10	36.21	1.00	1.56

注：YEAR为生存时间；SURVIVAL为生存率

根据表2中的数据，以YEAR为横坐标，SURVIVAL为纵坐标，其散点图见图3A；以lnYEAR为横坐标，lnSURVIVAL为纵坐标，其散点图见图3B。图3A可见，SURVIVAL呈指数下降，将术后YEAR和SURVIVAL都取自然对数后，lnYEAR与lnSURVIVAL呈现一个线性下降的趋势（图3B）。这种情况在生存率分析中常见，称为二次对数生存曲线图（LLS），可用来判断Cox比例风险模型的等比例假设。

点击查看大图

图3

某医院住院手术的715例乳腺癌患者术后生存时间与生存率自然对数转换前后的散点图　图A为术后生存时间与生存率的散点图；图B为术后生存时间自然对数值与生存率自然对数值的散点图

点击查看大图

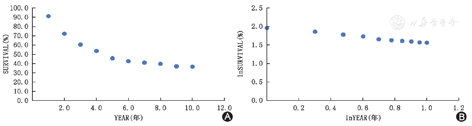
YEAR：生存时间；SURVIVAL：生存率

图3

某医院住院手术的715例乳腺癌患者术后生存时间与生存率自然对数转换前后的散点图　图A为术后生存时间与生存率的散点图；图B为术后生存时间自然对数值与生存率自然对数值的散点图

简单线性回归方程为：Y_i=α+βX_i+ε_i，α为截距，表示当自变量X为0时，因变量Y的平均估计值；回归系数β表示当X增加或减少1个单位时，Y的平均估计值改变量。

当自变量取自然对数时，这种对β的直观解释依然可行，表示当X增加或减少1个自然对数单位时，Y的平均估计值（）改变量；当因变量取自然对数时，β表示当X增加或减少1个单位时，自然对数改变量；当自变量和因变量都取自然对数时，β表示当X增加或减少1个自然对数单位时，自然对数改变量。

将回归系数β直接解释为自然对数改变量固然可以，但有时我们在对自变量和/或因变量进行对数转化后，仍需要用原X和Y来解释回归方程和回归系数，而非用对数单位的形式。这时不能简单地将X和Y取反对数，而是用百分比改变（percentage changes）来解释。下面结合实例1~3，分别对linear-log转换、log-linear转换和log-log转换（ln=log_e）进行详尽的阐述。

在进行线性回归时，如果数据不满足线性、独立、正态和方差齐的条件，可对数据进行转换，如对数转换、倒数转换、平方根转换等，使数据满足或近似符合线性条件，或改用其他统计分析方法^[3]。对数转换是常用的数据转换方法，可对自变量取对数、因变量取对数或两者都取对数，构建的分别是linear-log转换、log-linear转换和log-log转换，以e为底的自然对数转化是常见的对数转化方法。

拟合对数转换的回归方程后，回归系数的解释依次为：linear-log转换的回归系数表示X的自然对数每增加1个单位，Y的平均估计值改变量；log-linear转换的回归系数表示X每增加一个单位，Y的平均估计值的自然对数改变量；log-log转换的回归系数表示X的自然对数每增加1个单位，Y的平均估计值的自然对数改变量。当要用X和/或Y，而不是X和/或Y的自然对数值来解释回归方程和系数时，不能简单地取X和/或Y的反对数，需要一些变换，用X和/或Y的百分比改变来表示。

对于linear-log转换，当X取自然对数时，实际为X增加171.828%时，其回归系数为Y的平均估计值（）改变量；若取X增加固定百分比（p%）时，的改变量（即回归系数）为。对于log-linear转换，当Y取自然对数时，回归系数表示X增加1个单位时，的百分比改变(e^b-1)×100%。对于log-log转换，其实就是linear-log转换和log-linear转换的结合，X和Y都只能用百分比改变解释，即当X增加p%时，回归系数可解释为Y的平均估计值（）百分比改变。在实际应用中，用X和/或Y自然对数值还是X和/或Y值来解释回归方程和系数，要根据专业特点和解释的合理性来确定。

本文资料拟合的是简单线性回归，自变量只有一个，实际中，应用更多的是多重线性回归，自变量有多个，如地区平均受教育程度、人均可支配收入、地区医务人员数量等，对MLR的回归系数的解释：在调整了地区平均受教育程度、人均可支配收入和地区医务人员数量后，即这些协变量保持恒定值不变，感兴趣的研究变量与因变量的回归关系，此时的回归系数是控制了一些协变量的结果。变量取对数后，对X和Y的解释与简单线性回归相同，只是在模型中控制了协变量。

另外，在进行线性回归分析时，如果对连续的自变量进行标准化，可计算标准化回归系数，比较其相对重要性；如果对标准化值（标准正态离差）再取自然对数，用X和/或Y标准正态离差单位改变或标准正态离差对数单位改变来解释回归方程和系数，此时的回归系数可比。

总之，在自变量和/或因变量取自然对数后，仍然用X和/或Y来解释回归方程和系数，需要用其百分比改变；模型拟合步骤、自变量纳入模型方法及模型拟合策略遵循多重线性回归的拟合方法^[2]。