
提出一种新型脉冲神经元模型及其网络,描述其建模方法,并用计算机模拟验证其性能。
在充分考虑生物学适应性(激活电位阈值和不应期开关),及其对尖峰放电脉冲产生及其传导的动态调节机制基础上,在新型脉冲神经元模型中引入了突出后电位多通道滤波器,实现了输出电流及神经元突触强度的动态调节。提出基于自适应最小均方(LMS)的误差反向传播(BP)学习算法,并将其应用于尖峰放电神经网络的调节。
在自发噪声下,新型脉冲神经元模型的尖峰放电间期信号直方图满足泊松分布。通过2个新型脉冲神经元的简单连接,可以形成多种复杂的尖峰放电模式。新型脉冲神经元模型具有自发本征噪声的特征,能够形成复杂的周期尖峰放电模式。对于输入噪声控制,该模型的不应期与门限电位适应性参数的稳定性较好。刺激电流-尖峰放电脉冲频率间的线性关系较好。
所提出的新型脉冲神经元模型在自发噪声条件下能产生多种模式的振荡和相干振荡,这与生物神经元极其相似,能实现复杂的噪声信号处理。所采用的具有不同频带的多通道突触后电位滤波器,能使一些突触后电位信号变得平稳。所提出的基于于自适应LMS的BP学习算法克服了尖峰放电信号的瞬态变化特性导致的误差驱动学习算法无法应用的问题。

版权归中华医学会所有。
未经授权,不得转载、摘编本刊文章,不得使用本刊的版式设计。
除非特别声明,本刊刊出的所有文章不代表中华医学会和本刊编委会的观点。
针对生物系统中神经细胞及其所构成的大脑和各类神经系统(如感觉、知觉和运动神经系统),人类不断从实验和理论层面进行探索和研究。这些研究所获得的实验数据和理论机制,是人工神经元及其网络相关研究的灵感源泉。如神经元的尖峰放电、状态与膜电位变化及其突触连接与调节机制、神经网络的结构分层与分级、感受野与投射野的关系、神经元组振荡、同步振荡和其动力学机制等,已在神经元及其网络的数学建模及相关学习算法的研究中被广泛模仿和应用。针对生物系统神经元及其网络的模仿,使人工神经元及其网络与算法更趋合理,从而能实现类神经和类脑的计算、表达和通信。
神经元是神经网络的最基本计算单元,其数学建模是神经网络及其学习算法实现的基础和关键。最简单的神经元模型是McCulloch-Pitts(M-P)神经元模型,也被称为第一代神经元。第一代神经元中,通过比较输入值与阈值,将神经元分成抑制和兴奋2种状态,分别用0和1来表示。此后,研究者使用0到1之间的单调函数(激励函数),如S型函数等,来表达神经元尖峰的放电速率,并通过尖峰放电速率定义神经元抑制或兴奋的状态。这种神经元模糊地表达抑制和兴奋状态,属于第二代神经元。近年来,研究者正在努力通过用简单的数学模型,构建神经元尖峰放电的动态过程,从而实现类神经元建模和类脑计算,为下一代人工神经网络的研究注入了新的活力[1]。随着新型脉冲神经元及其网络与相关学习算法的出现[2],以及研究者对人工神经网络的结构和连接方式研究的深入(深度越来越深、稀疏度越来越稀、混合和堆叠越来越复杂),未来智能计算能力将越来越强大,泛化能力将越来越广泛[3,4]。
本研究中,提出了一个具有生物学合理性和解释性的神经元及其网络的数学建模方法。在一种简单的神经元模型基础上,提出了基于突触前、后电位的自适应学习算法。用计算机模拟的方法,对所提出的模型和算法进行了验证。结果表明,该模型和算法在类脑建模和类脑计算方面具有有效性和可用性。
为不失一般性,用mp(t)表示神经元膜电位的动态信号,其由3部分组成:恒定不变的静息(resting)膜电位Urest;神经元放电尖峰(spiking)电位sp(t);尖峰后膜电位psmp(t)。三者的关系为:mp(t)=sp(t)+psmp(t)。可将sp(t)看成超窄脉冲信号,即其动态时间远远短于psmp(t)信号。
如图1A所示,处于静息状态(resting)的神经元经历去极化(depolarization)瞬态过程达到峰值电位;再经历复极化(repolarization)瞬态过程到达超极化(hyperpolarization)电位,过程中产生尖峰放电;放电后的信号再从超极化电位经过一个动态过程恢复到静息状态;从超极化恢复到静息状态的过程中,存在一个不应期时间窗口。图1B中显示的波形图1A的合理近似,其中红色为尖峰电位,绿色为超极化电位,浅绿色为静息电位。如果信号采样周期大于尖峰脉冲宽度,那么尖峰电位可以表示成冲激信号δ(t),如图1C所示。
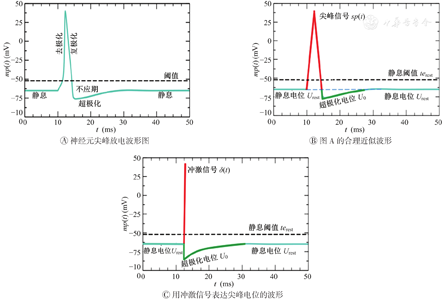

因此,物神经元的psmp(t)可以描述成在一定时间内从超极化电位U0恢复成静息电位Urest且逐渐增强的时变信号;在理想情况下,sp(t)可被视作冲激信号δ(t);而psmp(t)可被视作一个因果性的指数变化信号。下面将在数学建模中充分考虑生物神经元的实际动态特性。
在神经元刺激不应期内,激活后的神经元膜电阻Rm跳变到0再逐渐恢复到初始水平,该动态过程可以表达成Rm×ear(t),其中ear(t)表示渐变信号(软信号)或开关信号(硬信号),如图2A所示。神经元阈值电位适应性存在动态调节过程,尖峰放电后的阈值电位te(t)会从静息阈值电位terest触发并跃升至超极化阈值电位te0,然后再渐渐恢复到te(t)。同时,放电阈值电位具有累积效应,即在上一次尖峰放电阈值电位的基础上,会叠加一个增量电位teadd,即te0=te(T)+teadd,如图2B所示。其中,T是上一次尖峰放电的时间。阈值电位适应性的存在使尖峰放电后的阈值在外部电流刺激下具有阈值升高的累积效应。


不失一般性,用psp(t)表示尖峰电位传导到突触后神经元所形成的突触后电位。尖峰电位沿着突触前神经元的轴突传输,经过突触传输到突触后神经元的树突,输入到突触后神经元胞体。一般来说,神经元轴突末梢是通过一个或多个突触与突触后神经元的树突连接,如图3A所示。尖峰电位的传输过程可以看成一个冲激响应为psp(t)的滤波器的滤波过程,轴突末梢与树突连接的结构和数量决定突触后电位的尖峰冲激响应滤波器特性,如图3B所示。psp(t)形状及其电位取决于神经元细胞类型和突触末梢连接状态,且其相对于尖峰存在一个延时,该延时与突触前神经元轴突的长短有关,即突触具有遵循Hebb学习规则及其衍生规则的可塑性,如图3C所示。
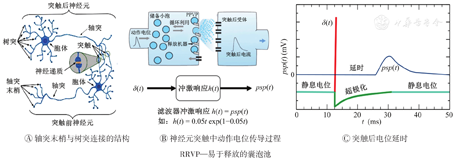

RRVP—易于释放的囊泡池
不失一般性,将神经元末梢表示为若干段单输入-多输出的等效电路网络,这些电路网络由电阻、电容、电流源和电压源组成,如图4A所示。由于电流源和电压源的偏置不会影响网络的滤波特性,因此电路网络可表示成由多个突触后电位滤波器构成的滤波器组,如图4B所示。通过上述建模过程,形成了一个新的、生物学可解释的、具有合理性的单输入-多输出神经元数学模型,其结构如图4C所示。与现有的人工神经元模型不同,该模型采用多输出的方式,即有多个不同的突触后电位滤波器,从而能产生不同频带的突触后电位,为解释脑电图(electroencephalogram,EEG)信号中经常出现的不同频带信号的整体振荡、同步振荡和振荡耦合等信号模式,提供了富有潜力的工具。该模型产生的动作电位由神经元本征噪声和动态信号耦合而成,其输出信号由尖峰电位激励滤波器组产生,等价于与神经末梢连接的突触的突触后电位。该模型中,具有不同频率特性的各突触后滤波器可以看成中心频率分频所用的带通滤波器,可以产生δ波(1~4 Hz)、θ波(4~8 Hz)、α波(8~14 Hz)、β波(14~30 Hz)、γ(30~80 Hz),以及其他带宽。与神经元胞体越近的末梢突触,其后电位信号带宽越宽;与神经元胞体越远的末梢突触,其带宽越窄。值得注意的是,神经元之间的连接往往不是通过一处神经末梢,而是包含了多个远近不同的连接点。当连接位置与神经元距离大到一定程度时,突触后电位滤波器的输出速率即为神经元的尖峰放电速率,此时网络输出就等价于传统神经网络的激励函数输出。另外,神经元的振荡、同步振荡,以及神经网络的通信和计算可以通过不同的连接方式实现,因此可实现大脑皮层不同频率的EEG信号之间的耦合。
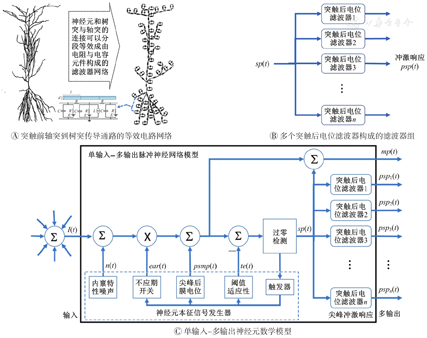

基于1.3节中所提出的神经元数学模型,构建脉冲神经网络的连接组件,组件参数为包括突触电导wij和尖峰脉冲传输延时dij。如图5A所示,突触前、后神经元由轴突上的突触连接,轴突和突触分别为连接的延时和权重元件,延时由轴突长度决定,电导由突触连接决定。通过学习算法,可产生不同的延时和电导,从而重塑连接网络。突触电导由2部分组成,分别为静息电导wijrest和激活电导wijact(t),wij(t)=wijrest+wijact(t)。激活电导具有动态累积特性,即每次尖峰放电时,突触电导就会累加一个增量wijadd,从而由静息电导跳变到激活电导,然后再逐渐恢复到静息电导,如图5B所示。这种动态短期增强的连接方式使网络在完成智能计算的同时,能够实现网络内部的短时记忆和通信,使网络具有振荡和相干振荡的通信能力。
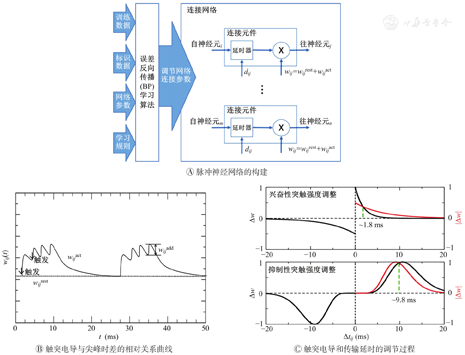

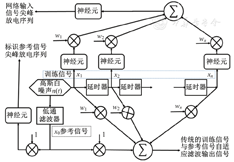
使用一种基于自适应最小均方(least mean square,LMS)算法[5]的误差反向传播(error back propagation,BP)学习算法对所提出的脉冲神经网络模型进行调节。该算法中,一方面分别将训练样本和参考样本中的由尖峰神经元输出的突触后电位信号作为自适应LMS算法的输入信号和参考信号,并混合使用自适应LMS算法和BP学习算法对深度神经网络进行训练;另一方面,根据训练样本和标识样本输出的尖峰时间,使用基于Hebb学习规则的尖峰时间依赖可塑性算法,精细调节连接强度和传输延时[6,7]。神经元之间由突触连接,连接强度决定神经元之间的信息沟通强度,连接强度的变化即为突触可塑性。利用尖峰时间依赖突触可塑性的突触电导与延迟的调节过程,如图5C所示。
计算机仿真中,神经元的静息膜电位为-70 mV,超极化膜电位为-80 mV,静息膜阈值电位为-60 mV,适应性膜阈值电位为-50 mV,适应性膜阈值电位累积量为10 mV,尖峰放电膜电位35 mV;神经元兴奋性绝对不应期和尖峰后膜电位动态时间均为5 ms,膜阈值电位动态时间为50 ms,突触后电位峰值时间为10 ms,突触后电位动态时间为50 ms;神经元的静息膜阻抗为100 MΩ:仿真计算步长为0.5 ms,时间为1 000 ms。不失一般性,神经元的时间动态特性的变化规律为
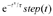
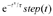
对于神经元的膜电位和不应期的动态特性,x=0.1;阈值电位,x=1。
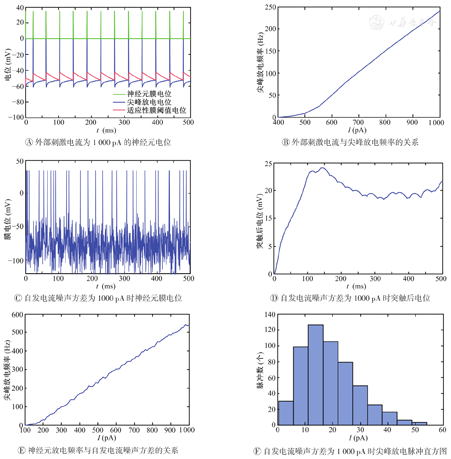
分别对外部刺激和本征噪声对神经元膜电位和尖峰放电频率的影响进行了仿真,获得了该模型的强迫周期性振荡和本征噪声泊松分布的尖峰放电特性,如图6所示。结果显示,神经元自发电流噪声方差为1 000 pA时,突触后电位低频信号变化范围为15~20 mV(图6D);神经元平均放电频率与自发电流噪声方差呈现近似线性的关系(图6E);与真实生物神经元的信号相比,所获得的尖峰放电脉冲间隔具有相同的泊松分布(图6F)。

2个神经元相互作用的仿真中,神经元的时间动态特性表达式中,x=1。仿真计算步长为0.5 ms,时间为10 000 ms。其他参数与2.1节中相同。
共考察了4种连接和激励方式下的2个神经元之间的相干振荡模式,如图7所示。其中,除图7C的输入为外部恒定电流刺激,其他均为神经元自发产生的噪声节律,即振荡与相干振荡。
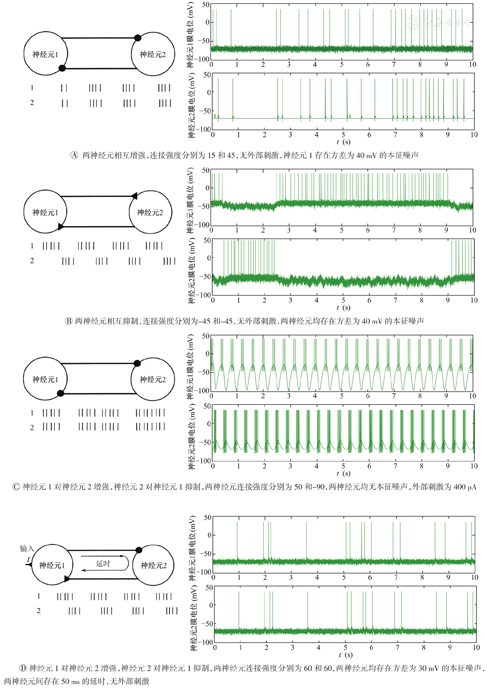

当2个神经元之间的连接条件为:相互增强的连接方式;两神经元连接强度分别为15和45;无外部刺激;仅有神经元1存在方差为40 mV的本征噪声。结果表明,此时两神经元之间存在神经系统中广泛出现的相干和爆发尖峰放电。(图7A)
当2个神经元之间的连接条件为:相互抑制的连接方式;连接强度分别为-45和-45;无外部刺激;两神经元均存在方差为40 mV的本征噪声。结果表明,此时神经元均广泛存在竞争性爆发放电。(图7B)
当2个神经元之间的连接条件为:神经元1对神经元2增强,神经元2对神经元1抑制;两神经元连接强度分别为50和-90;两神经元均无本征噪声;外部刺激为400 pA。结果表明,此时神经元广泛存在节律性爆发放电。(图7C)
当2个神经元之间的连接条件为:神经元1对2增强,神经元2对神经元1抑制;两神经元连接强度分别为60和60;两神经元均存在方差为30 mV的本征噪声;两神经元间存在50 ms的延时;无外部刺激。结果表明,此时两神经元之间广泛存在相干和爆发尖峰放电。(图7D)
上述仿真结果表明,本研究中提出的神经元模型在构建不同节律的神经活动方面具有很强的灵活性。
神经元网络相互作用的仿真中,突触后电位峰值时间为50 ms,其动态时间为10 ms。神经元的时间动态特性表达式中,x=1。仿真计算步长为0.5 ms,时间为2 000 ms。其他参数与2.1节中相同。
神经元之间的连接为侧向抑制的墨西哥帽函数,即每个神经元与其相邻的神经元是兴奋性连接,而对远端的神经元是抑制性连接,每个神经元都自发出独立、不相关的高斯白噪声。仿真结果表明,32个神经元具有爆发振荡的能力,神经元之间产生相干性爆发尖峰放电,即同步振荡,如图8所示。神经网络的侧向抑制具有处理复杂环境噪声的能力,可有效地模拟神经生理节律。


为了便于比较,训练样本和参考样本均通过同一个高斯白噪声信号源产生。如图9所示,一路白噪声信号经过低通滤波器后形成参考样本,另一路白噪声信号经过若干延时器后形成用于单层感知器训练的小样本。感知器经过基于自适应LMS的BP学习算法的训练,可以实现训练样本与参考样本的尖峰脉冲相干(图10A)。此外,通过调整模型参数,可以产生相干的爆发尖峰脉冲,如图10B和图10C所示。因此,这种脉冲神经网络具有拟线性,其训练方法易推广到多层感知器和卷积神经网络的学习训练中。

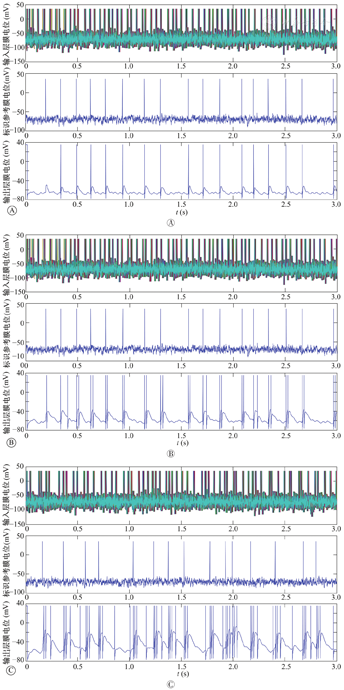

仿真结果表明:①新型脉冲神经元模型具有参数可解释的生物学合理性,该模型在自发噪声下,其尖峰放电间期的信号直方图满足泊松分布,与真实生物神经细胞的尖峰放电间期信号的统计学分布规律相似。②通过2个新型脉冲神经元的简单连接,可以形成多种复杂的尖峰放电模式,在类脑建模和计算中有潜在价值。③与微分方程描述的神经元模型相比[8],新型脉冲神经元模型具有自发本征噪声的特征,能够形成复杂的周期尖峰放电模式。④与采用微分方程描述的神经元模型相比,新型脉冲神经元模型的不应期与门限电位适应性参数在输入噪声控制方面的稳定性更好,刺激电流与尖峰放电脉冲频率间的线性关系更好,且其信号在自发噪声的情况下更为平滑。
目前普遍认为,振荡及其同步模式对于信息处理和功能控制有重要影响,如感官知觉、行为、呼吸和认知等。尤其在大脑的特征提取、计算和整合捆绑方面,振荡和相干振荡具有重要的意义。振荡模式是由神经元之间的特定连接方式决定的,是由特定神经元的固有周期性产生的,这一核心问题往往尚未得到解决。
有研究结果表明,很多生物中的神经是由相互耦合的振荡器组成的群体。本研究中提出的新型脉冲神经元模型在自发噪声条件下能产生多种模式的振荡和相干振荡,这与生物神经元极其相似,能实现复杂的噪声信息处理。
由于所提出的新型脉冲神经元模型采用了具有不同频带的多通道突触后电位滤波器,使一些突触后电位信号变得平稳。此外,所提出的基于自适应LMS的BP学习算法克服了尖峰放电信号的瞬态变化特性导致的误差驱动的学习算法无法应用的问题[9,10]。更为重要的是,新型脉冲神经元模型中,不同频率特征滤波器能模仿大脑产生类脑驱动,即可模仿人体运动的肌电驱动方式,这是现有神经元模型所不及的。
所有作者均声明不存在利益冲突



























